Единица измерения дбм: Измерения. Единицы измерения. Децибелы — универсальная мера
Измерения. Единицы измерения. Децибелы — универсальная мера
ПРИМЕНЕНИЕ ДЕЦИБЕЛ В РАДИОЭЛЕКТРОНИКЕ И ЭЛЕКТРОАКУСТИКЕ
ЧТО ТАКОЕ ДЕЦИБЕЛЫ?
Универсальные логарифмические единицы децибелы широко используются при количественных оценках параметров различных аудио и видео устройств в нашей стране и за рубежом. В радиоэлектронике, в частности, в проводной связи, технике записи и воспроизведения информации децибелы являются универсальной мерой.
Децибел — не физическая величина, а математическое понятие
В электроакустике децибел служит по существу единственной единицей для характеристики различных уровней — интенсивности звука, звукового давления, громкости, а также для оценки эффективности средств борьбы с шумами.
Децибел — специфическая единица измерений, не схожая ни с одной из тех, с которыми приходится встречаться в повседневной практике. Децибел не является официальной единицей в системе единиц СИ, хотя, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
Децибел — не физическая величина, а математическое понятие.
В этом отношении у децибел есть некоторое сходство с процентами. Как и проценты, децибелы безразмерны и служат для сравнения двух одноименных величин, в принципе самых различных, независимо от их природы. Следует отметить, что термин «децибел» всегда связывают только с энергетическими величинами, чаще всего с мощностью и, с некоторыми оговорками, с напряжением и током.
Децибел (русское обозначение — дБ, международное — dB) составляет десятую часть более крупной единицы — бела1.
Бел — это десятичный логарифм отношения двух мощностей. Если известны две мощности Р1 и Р2, то их отношение, выраженное в белах, определяется формулой:

Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п.
Напомним вкратце, что такое логарифм. Любое положительное2 число, как целое, так и дробное, можно представить другим числом в определенной степени.
Так, например, если 102 = 100, то 10 называют основанием логарифма, а число 2 — логарифмом числа 100 и обозначают log10 100=2 или lg 100 = 2 (читается так: «логарифм ста при основании десять равен двум»).
Логарифмы с основанием 10 называются десятичными логарифмами и применяются чаще всего. Для чисел, кратных 10, этот логарифм численно равен количеству нулей за единицей, а для остальных чисел вычисляется на калькуляторе или находится по таблицам логарифмов.
Логарифмы с основанием е = 2,718… называются натуральными. В вычислительной технике обычно применяются логарифмы с основанием 2.
Основные свойства логарифмов:

Разумеется, эти свойства справедливы и для десятичных и натуральных логарифмов. Логарифмический способ представления чисел часто оказывается очень удобным, так как позволяет подменять умножение — сложением, деление — вычитанием, возведение в степень умножением, а извлечение корня — делением.
На практике бел оказался слишком крупной величиной, например, любые отношения мощностей в границах от 100 до 1000 укладываются в пределах одного бела — от 2 Б до 3 Б. Поэтому для большей наглядности решили число, показывающее количество бел, умножать на 10 и полученное произведение считать показателем в децибелах, т. е., например, 2 Б = 20 дБ, 4,62 Б = 46,2 дБ и т. д.
Обычно отношение мощностей выражают сразу в децибелах по формуле:

Действия с децибелами не отличаются от операций с логарифмами.
Нетрудно посчитать, что 1 дБ соответствует отношению мощностей примерно равному 1,259 или 26%.
2 дБ = 1 дБ + 1 дБ → 1,259 * 1,259 = 1,585;
3 дБ → 1,2593 = 1,995;
4 дБ → 2,512;
5 дБ → 3,161;
6 дБ → 3,981;
7 дБ → 5,012;
8 дБ → 6,310;
9 дБ → 7,943;
10 дБ → 10,00.
Знак → означает «соответствует».
Подобным образом можно составить таблицу и для отрицательных значений децибел. Минус 1 дБ характеризует убывание мощности в 1/0,794 = 1,259 раза, т. е. тоже примерно на 26%.
Запомните, что:
⇒ Если Р2=Р1 т. е. P2 /P1=1, то NдБ = 0, так как lg 1=0.
⇒ Если P2 > Pl, то число децибел положительно.
⇒ Если Р2 < P1, то децибелы выражаются отрицательными числами.
Положительные децибелы часто называют децибелами усиления. Отрицательные децибелы, как правило, характеризуют потери энергии (в фильтрах, делителях, длинных линиях) и называются децибелами затухания или потерь.
Между децибелами усиления и затухания существует простая зависимость: одинаковому числу децибел с разными знаками соответствуют обратные числа отношений. Если, например, отношению Р2/Р1 = 2 → 3 дБ, то –3 дБ → 1/2, т. е. 1 / Р2/Р1 = Р1/Р2
⇒ Если Р2/Р1 представляет степень десяти, т. е. Р2/Р1 = 10k, где k — любое целое число (положительное или отрицательное), то NдБ = 10k, так как lg 10k = k.
⇒ Если Р2 или Р1 равно нулю, то выражение для NдБ теряет смысл.
И еще одна особенность: кривая, определяющая значения децибел в зависимости от отношений мощностей, вначале быстро растет, затем ее рост замедляется.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы
К достоинствам системы децибел относят:
⇒ универсальность, т. е. возможность использования при оценке различных параметров и явлений;
⇒ огромные перепады преобразуемых чисел — от единиц и до миллионов — отображаются в децибелах числами первой сотни;
⇒ натуральные числа, представляющие степени десяти, выражаются в децибелах числами, кратными десяти;
⇒ взаимообратные числа выражаются в децибелах равными числами, но с разными знаками;
⇒ в децибелах могут быть выражены как отвлеченные, так и именованные числа.
К недостаткам системы децибел относят:
⇒ малую наглядность: для преобразования децибел в отношения двух чисел или выполнения обратных действий требуется проведение расчетов;
⇒ отношения мощностей и отношения напряжений (или токов) пересчитываются в децибелы по разным формулам, что иногда ведет к ошибкам и путанице;
⇒ децибелы могут отсчитываться только относительно не равного нулю уровня; абсолютный нуль, например 0 Вт, 0 В, децибелами не выражается.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы.
Сравнение двух сигналов путем сопоставления их мощностей не всегда бывает удобным, так как для непосредственного измерения электрической мощности в диапазоне звуковых и радиочастот требуются дорогие и сложные приборы. На практике при работе с аппаратурой гораздо проще измерять не мощность, которая выделяется на нагрузке, а падение напряжения на ней, а в некоторых случаях — протекающий ток.
Зная напряжение или ток и сопротивление нагрузки, легко определить мощность. Если измерения проводятся на одном и том же резисторе, то:

Этими формулами очень часто пользуются практике, но обратите внимание, что если напряжения или токи измеряются на разных нагрузках, эти формулы не работают и следует использовать другие, более сложные зависимости.
Пользуясь приемом, который был использован при составлении таблицы децибел мощности, можно аналогично определить, чему равен 1 дБ отношения напряжений и токов. Положительный децибел будет равен 1,122, а отрицательный децибел будет равен 0,8913, т.е. 1 дБ напряжения или тока характеризует возрастание или убывание этого параметра примерно на 12% по отношению к первоначальному значению.
Формулы выводились в предположении, что сопротивления нагрузок имеют активный характер и между напряжениями или токами нет фазового сдвига. Строго говоря, следовало бы рассматривать общий случай и учитывать для напряжений (токов) наличие угла сдвига по фазе, а для нагрузок не только активное, но полное сопротивление, включая и реактивные составляющие, однако это существенно только на высоких частотах.
Полезно запомнить некоторые часто встречающиеся на практике значения децибел и характеризующие их отношения мощностей и напряжений (токов), приведенные в табл. 1.
Таблица 1. Часто встречающиеся значения децибел мощности и напряжения
|
± дБ |
1 |
3 |
10 |
20 |
30 |
|
|
Р2/Р1 |
1,26 (0,79) |
2 (0,5) |
10 (0,1) |
100 (0,01) |
1000 (0,001) |
|
|
± дБ |
1 |
3 |
6 |
10 |
20 |
40 |
|
U2/U1 или I2/I1 |
1,12 (0,9) |
1,41 (0,707) |
2 (0,5) |
3,16 (0,316) |
10 (0,1) |
100 (0,01) |
Пользуясь этой таблицей и свойствами логарифмов легко подсчитать, чему соответствуют произвольные значения логарифм. Например, 36 дБ мощности можно представить как 30+3+3, что соответствует 1000*2*2 = 4000. Тот же самый результат мы получим, представив 36 как 10+10+10+3+3 → 10*10*10*2*2 = 4000.
СОПОСТАВЛЕНИЕ ДЕЦИБЕЛ С ПРОЦЕНТАМИ
Ранее отмечалось, что понятие децибел имеет некоторое сходство с процентами. Действительно, так как в процентах выражается отношение какого-то числа к другому, условно принятому за сто процентов, отношение этих чисел также можно представить в децибелах при условии, что оба числа характеризуют мощность, напряжение или ток. Для отношения мощностей:

Для отношения напряжений или токов:

Можно также вывести формулы для пересчета децибел в проценты отношения:

В табл. 2 дан перевод некоторых, наиболее часто встречающихся значений децибел в проценты отношений. Различные промежуточные значения можно найти по номограмме на рис. 1.

Рис. 1. Перевод децибел в проценты отношений по номограмме
Таблица 2. Перевод децибел в проценты отношений
|
% |
100 |
50 |
10 |
1 |
0,1 |
|
NU или NI |
0 |
-6 |
-20 |
-40 |
-60 |
|
NP |
0 |
-3 |
-10 |
-20 |
-30 |
Рассмотрим два практических примера, поясняющих перевод процентного отношения в децибелы.
Пример 1. Какому уровню гармоник в децибелах по отношению к уровню сигнала основной частоты соответствует коэффициент нелинейных искажений в 3%?
Воспользуемся рис. 1. Через точку пересечения вертикальной линии 3% с графиком «напряжение» проведем горизонтальную линию до пересечения с вертикальной осью и получим ответ: –31 дБ.
Пример 2. Какому ослаблению напряжения в процентах соответствует его изменение на –6 дБ?
Ответ. На 50% первоначальной величины.
В практических расчетах дробную часть численного значения децибел часто округляют до целого числа, однако при этом в результаты расчетов вносится дополнительная погрешность.
ДЕЦИБЕЛЫ В РАДИОЭЛЕКТРОНИКЕ
Рассмотрим несколько примеров, поясняющих методику использования децибел в радиоэлектронике.
Затухание в кабеле
Потери энергии в линиях и кабелях на единицу длины характеризуются коэффициентом затухания α, который при равном входном и выходном сопротивлениях линии определяется в децибелах:

где U1 — напряжение в произвольном сечении линии; U2 — напряжение
Децибел — Википедия
Децибе́л (русское обозначение: дБ; международное: dB) — дольная единица бела, равная одной десятой этой единицы. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения.
Отношение DP{\displaystyle D_{P}} двух значений энергетической величины P{\displaystyle P}, такой как мощность, энергия, плотность энергии и т. п., выраженное в децибелах, определяется по формуле:
- DP=10lgP2P1.{\displaystyle D_{P}=10\lg {\frac {P_{2}}{P_{1}}}.}
Отсюда следует, что увеличение энергетической величины на 1 дБ означает её увеличение в 100,1{\displaystyle 10^{0,1}} ≈ 1,259 раза.
Энергетические величины пропорциональны квадратам силовых величин (или величин поля, как принято в международных документах[1][2]), таких как звуковое давление, электрическое напряжение, сила электрического тока и т. п., поэтому отношение DF{\displaystyle D_{F}} двух значений силовой величины F{\displaystyle F}, выраженное в децибелах, определяется по формуле:
- DF=20lgF2F1.{\displaystyle D_{F}=20\lg {\frac {F_{2}}{F_{1}}}.}
Отсюда следует, что увеличение силовой величины на 1 дБ означает её увеличение в 100,05{\displaystyle 10^{0,05}} ≈ 1,122 раза.
Децибел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ[3]. В основном применяется в электросвязи, акустике, радиотехнике, в теории систем автоматического управления[4][5][6].
История
Распространение децибела берёт начало от методов, используемых для количественной оценки потери (ослабления) сигнала в телеграфных и телефонных линиях. Единицей потерь изначально была миля стандартного кабеля (англ. mile of standard cable — m.s.c.). 1 m.s.c. соответствовала потерям мощности сигнала с частотой 800 Гц в кабеле длиной в 1 милю (примерно 1,6 км), имеющем распределённое сопротивление 88 Ом (на петлю) и распределённую ёмкость 0,054 мкФ[7] (диаметр жил витой пары около 0,9 мм). Такая величина потерь была близка к наименьшей различимой средним слушателем разнице двух сигналов по громкости. Однако миля стандартного кабеля была частотно-зависимой, и она не могла быть полноценной единицей отношения мощностей[8].
В 1924 году компания «Белл телефон» получила положительный ответ на новое определение единицы среди членов Международного телеграфного союза в Европе: вместо m.s.c. — единица передачи (англ. transmission unit — TU). Единица передачи определялась так, что численное выражение в этих единицах соответствовало десяти десятичным логарифмам отношения измеренной мощности к исходной мощности[9]. Удобство такого определения было в приблизительном соответствии старой и новой единиц (1 m.s.c. — это примерно 0,95 TU). В 1928 году компания «Белл телефон» переименовала единицу передачи TU в децибел[10], который стал одной десятой вновь определённой единицы логарифмического отношения мощностей, получившей наименование бел в честь американского учёного Александра Белла[11].
Единица бел используется редко, в то время как децибел получил широкое распространение[12].
Изначальное определение децибела в Ежегоднике стандартов Национального института стандартов и технологий в США от 1931 года[13]:
Децибел может быть определён таким утверждением, что две величины мощности отличаются на 1 децибел, когда они находятся в соотношении 100,1, и любые две величины мощности отличаются на N децибел, когда они находятся в соотношении 10N(0,1). Количество единиц передачи (децибелов), выражающее отношение любых двух мощностей, в десять раз превышает десятичный логарифм этого отношения.
Оригинальный текст (англ.)
The decibel may be defined by the statement that two amounts of power differ by 1 decibel when they are in the ratio of 100.1 and any two amounts of power differ by N decibels when they are in the ratio of 10N(0.1). The number of transmission units expressing the ratio of any two powers is therefore ten times the common logarithm of that ratio.
В апреле 2003 года Международный комитет мер и весов (МКМВ) рассматривал рекомендацию о включении децибела в Международную систему единиц (СИ), но отказался от этого предложения[14]. Однако децибел признан другими международными организациями, такими как Международная электротехническая комиссия (МЭК) и Международная организация по стандартизации (ИСО)[15]. МЭК позволяет использовать децибел и с силовыми, и с энергетическими величинам, и этой рекомендации следуют многие национальные организации по стандартизации.
Определение
Децибелы принято использовать для измерения или выражения отношения одноимённых энергетических величин, таких как мощность, энергия, интенсивность, плотность потока мощности, спектральная плотность мощности и т. п., а также силовых величин, таких как напряжение, сила тока, напряженность поля, звуковое давление и т. п. Часто в качестве одной из величин отношения (в знаменателе) выступает общепринятая исходная (или опорная) величина. Тогда отношение, выраженное в децибелах, принято называть уровнем соответствующей физической величины (например, уровень мощности, уровень напряжения и т. д.)[1][2].
Энергетические величины
| D{\displaystyle D} | P2/P1{\displaystyle P_{2}/P_{1}} | F2/F1{\displaystyle F_{2}/F_{1}} |
|---|---|---|
| 40 dB | 10000 | 100 |
| 20 dB | 100 | 10 |
| 10 dB | 10 | ≈ 3,16 |
| 6 dB | ≈ 4 | ≈ 2 |
| 3 dB | ≈ 2 | ≈ 1,41 |
| 1 dB | ≈ 1,26 | ≈ 1,12 |
| 0 dB | 1 | 1 |
| −1 dB | ≈ 0,79 | ≈ 0,89 |
| −3 dB | ≈ 0,5 | ≈ 0,71 |
| −6 dB | ≈ 0,25 | ≈ 0,5 |
| −10 dB | 0,1 | ≈ 0,32 |
| −20 dB | 0,01 | 0,1 |
| −40 dB | 0,0001 | 0,01 |
Отношение DP{\displaystyle D_{P}} двух значений энергетической величины P2{\displaystyle P_{2}} и P1{\displaystyle P_{1}}, выраженное в децибелах, определяется по формуле:
- DP=10lgP2P1.{\displaystyle D_{P}=10\lg {\frac {P_{2}}{P_{1}}}.}
Отсюда:
- P2P1=100,1DP{\displaystyle {\frac {P_{2}}{P_{1}}}=10^{0,1D_{P}}} 00или00 P2=P1⋅100,1DP.{\displaystyle P_{2}=P_{1}\cdot 10^{0,1D_{P}}.}
Силовые величины
Энергетические величины пропорциональны квадратам силовых величин. Например, в электрической цепи мощность P{\displaystyle P}, рассеиваемая в тепло на нагрузке с сопротивлением R{\displaystyle R} при напряжении U{\displaystyle U}, определяется по формуле:
- P=U2R.{\displaystyle P={U^{2} \over R}.}
Отсюда отношение двух величин:
- P2P1=U22R2R
как перевести из дБм в дБ? (часть 2)
На многих форумах люди задают вопрос: как перевести из дБ в дБм?
Как было показано выше, преимущество логарифмической шкалы очевидно в случае, когда мы исследуем во сколько раз значение одной величины больше или меньше другой.
Например, потери на элементе ВОЛС (в сплиттере, в ОВ или механическом соединителе) определяются соотношением:
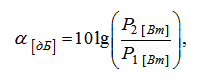
где P1 и P2 – мощности сигнала соответственно на входе и выходе элемента, выраженные в Вт, мВт (mВт, милливатт) или мкВт (μВт, микроватт).
Помимо дБ, существует еще одна похожая логарифмическая единица измерения – дБм. В отличие от дБ, которые характеризуют потери (во сколько раз уменьшается мощность оптического сигнала) или усиление (во сколько раз увеличивается мощность оптического сигнала), дБм показывают уровень мощности сигнала, относительно опорной мощности равной 1 мВт.
Перевод мощности сигнала из мВт в логарифмическую шкалу – дБм, производится измерителем оптического излучения по формуле
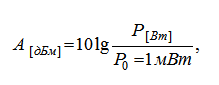 (2.1)
(2.1)
где P0=1 мВт – абсолютный нулевой уровень, рекомендованный МСЭ-Т (международным союзом электросвязи, сектором стандартизации). Буква «м», добавленная после дБ, означает, что в качестве опорного уровня мощности взят 1 мВт. Если качестве опорного уровня мощности взять 1 мкВт, то обозначение будет иметь вид дБмк. В англоязычной литературе часто dBm обозначают dBmW, (переводя на рус. – дБмВт), акцентируя внимание на то, что дБ взят по мощности, а не по напряжению или току. Для сокращения записи обычно Вт опускают, и остается просто дБм.
Может возникнуть вопрос, зачем мощность сигнала переводить в дБм? Ответ очевиден – чтобы можно было при расчетах оперировать с дБ и в результате возникающих в линии связи (проводной или беспроводной) потерь и усилений сигнала вычислить его уровень на входе приемника.
Хорошо, почему тогда в качестве опорного уровня принят 1 мВт, не проще было бы взять P0=1 Вт и уровень сигнала отображать также в дБ? Согласно ОСТ 45.159-2000, децибел – это логарифмическая единица уровней, затуханий и усилений. Поэтому уровень сигнала также можно выражать в дБ, только в этом случае, по-видимому, чтобы не путать уровень сигнала с потерями используют обозначение дБВт (англ. dBW)
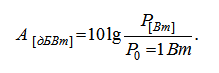 (2.2)
(2.2)
Обратное преобразование из дБВт в Вт осуществляется по следующей формуле:
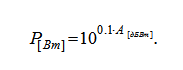
Почему в качестве опорного уровня принят 1 мВт? Честно говоря, ответ на этот вопрос нигде не встречается. На наш взгляд это значение используется в силу следующих обстоятельств.
Единица измерения дБм используется в радиотехнике, СВЧ-технике и волоконно-оптических системах передачи в качестве удобной меры уровня мощности сигнала. При выражении величины мощности в дБм в качестве нулевого отсчета берется опорная мощность P0=1 мВт, т.е. сигнал с мощностью P=1 мВт соответствует 0 дБм. В радиосвязи и ВОЛС используются сигналы, мощность которых лежит приблизительно как раз в районе 1 мВт. Например, при организации с помощью ноутбуков беспроводной локальной сети типичная мощность излучаемого радиосигнала составляет 32 мВт. В оптическом канале максимальная мощность ограничена, с одной стороны, возможностью возникновения нелинейных эффектов, с другой – соображениями лазерной безопасностью. Лазером в 500мВт можно ослепить летчика самолета. Максимальная мощность группового оптического сигнала в интерфейсе MRI-SM не должна превышать 50 мВт (уровень мощности P0max = 17 дБм). Выходная мощность генераторов сигнала простирается обычно от -140 дБм до +20 дБм или от 0,01 фВт (фемто Ватт) до 0,1 Вт. Базовые станции сотовой связи осуществляют передачу сигналов примерно на уровне +43 dBm или 20 Вт. Уровень сигнала мобильных телефонов лежит в пределах от +10 дБм до +33 дБм или от 10 мВт до 2 Вт. Вещательные передатчики работают в пределах от +70 дБм до +90 дБм или от 10 кВт до 1 МВт.
В связи с этим, если бы мы для отображения уровня сигнала использовали дБВт, то нам пришлось бы работать с отрицательными величинами: 1 мВт соответствует минус 30 дБВт, 50 мВт соответствует минус 13 дБВт. Очевидно, это вызывает некоторую путаницу – большая мощность соответствует меньшему уровню сигнала. Таким образом, выражение уровня мощности в дБм в системах телекоммуникаций в большинстве случаев является более удобным, нежели дБВт.
Возможно также, что выбор опорной мощности в 1 мВт появился в результате следующих обстоятельств. Исторически сложилось в качестве действующего значения опорного напряжения в канале передачи брать 0.775 В (из ранних телефонных стандартов), а в качестве нагрузки 600 Ом (сопротивление катушек приемного электромагнита у аппарата Морзе). В этом случае рассеиваемая мощность на нагрузке будет составлять 1 мВт.
-
Довольно часто, наравне с децибелами применяются неперы. Непер – логарифмическая величина (натуральный логарифм безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную). Своё название данная единица получила в честь математика, «изобретателя логарифмов» Джона Непера.
-
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
-
При некотором навыке операции с децибелами вполне реально выполнять в уме. Для этого полезно помнить следующие взаимосвязи:
1 дБ – в 1.25 раза,
3 дБ – в 2 раза,
10 дБ – в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ – в 2·2 = в 4 раза,
12 дБ = 4 · (3 дБ) – в 24 = в 16 раз
а также:
13 дБ = 10 дБ + 3 дБ – в 10·2 = в 20 раз,
20 дБ = 10 дБ + 10 дБ – в 10·10 = в 100 раз,
и т.д.
Децибел — это… Что такое Децибел?
Децибе́л — логарифмическая единица уровней, затуханий и усилений.[1]
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять:
где AdB — величина в децибелах, A — измеренная физическая величина, A0 — величина, принятая за базис.
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трёхкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причём к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB»[2] (неправильно: дб, Дб).
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международное бюро мер и весов рекомендовала включить его в эту систему.
Сравнение с другими логарифмическими единицами
| название | сокращение | соответствует изменению в … раз | пересчёт в … | |||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | Xm | |||
| децибел | дБ, dB | ≈1,26 () | 1 | 0,1 | ≈0,115 | −0,25 |
| бел | Б, B | 10 | 10 | 1 | ≈1,15 | −2,5 |
| непер | Нп, Np | ≈2,72 (e) | ≈8,686 | ≈0,8686 | 1 | ≈−1,086 |
| звёздная величина | Xm | ≈0,398 () | −4 | −0,4 | ≈−0,921 | 1 |
Области применения
Децибелы широко применяются в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибелы используются не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). В децибелах можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
Переход к децибелам
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P ~ U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические.[источник не указан 153 дня]
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:
- ,
где x — величина, измеряемая в дБ; P1/P0 — отношение значений двух мощностей: измеряемой P1 к так называемой опорной P0, то есть базовой, взятой за нулевой уровень (имеется в виду нулевой уровень в единицах дБ, поскольку в случае равенства мощностей P1 = P0 логарифм их отношения lg(P1/P0) = 0).
Соответственно, переход от дБ к отношению мощностей осуществляется по формуле:
- ,
где x — величина, измеряемая в дБ. Мощность P1 может быть найдена при известной опорной мощности P0 по выражению
Оптический бюджет и мощность дБм


Search
 +7 (812) 244-57-09
+7 (812) 244-57-09


0
Сравнить
0
Wishlist
0 items
/
0 ₽
Меню
КАТАЛОГ ПРОДУКЦИИ
- Smart SFP
- Трансиверы
- SFP модули
- Одноволоконные
- Двухволоконные
- CWDM
- DWDM
- SFP+ модули
- Одноволоконные
- Двухволоконные
- CWDM
- DWDM
- XFP модули
- Одноволоконные
- Двухволоконные
- CWDM
- DWDM
- RJ-45 модули
- SFP28 модули
- QSFP+ и QSFP28 модули
- CFP модули
- X2 и XENPAK модули
- SFP модули
- Кабели AOC и DAC
- Оптические усилители
- DWDM усилители
- CATV усилители
- PON+CATV усилители
- Мультиплексоры
- Оптические фильтры
- Компенсаторы дисперсии
- Транспондеры
- Медиаконвертеры
- Одноволоконные
- Двухволоконные
- С SFP портом
- С USB портом
- 10G
- Сетевые карты
- Оптические делители
- FBT делители
- PLC делители
- Расходные материалы
- Адаптеры
- Аттенюаторы
- Патч-корды
- Пигтейлы
- ADVA
- О компании ADVA
- FSP 3000
- Терминалы FSP 3000
- Компоненты FSP 3000
- ALM
- Компоненты ALM
- TeraFlex
- MicroMux
- Smart SFP
- Smart SFP CSOP
- Smart SFP TPOP
- Smart SFP TSOP
- Smart SFP+ TSOP
- Доставка
- Оплата
- Гарантия
- Услуги
- Перепрошивка трансиверов
- Подбор оптического оборудования
- Бесплатное тестирование
- Блог
- Новости
- Обзоры
- Wiki
- Трансиверы
- Активные компоненты
- Пассивные компоненты
- Системы уплотнения
что такое мВт (mW); дБ (dB); дБм (dBm); дБи (dBi)
мВт (mW) — милливатт (то есть 1/1000 ватта) — единица измерения мощности вообще и мощности радиосигнала в частности. Величина абсолютная.
Может иметь значения от 0 и до очень больших величин.
дБ (dB) — децибелл — логарифмическая единица уровней, затуханий и усилений. Применительно к нашей тематике, это коэффициент усиления или, наоборот, затухания мощности сигнала. Величина относительная.
Может иметь как положительные, так и отрицательные значения.
где P(изм) — измеряемая мощность, а P(оп) — опорная мощность, то есть та, по сранению с которой мы хотим измерить P(изм).
дБи (dBi) — это децибелл по сравнению с «i», то есть по отношению к изотропоному излучателю — идеальной антенне, диаграмма направленности которой представляет собой сферу, коэффициент усиления которой равен единице и КПД которой равен 100%. Естественно, изотропный излучатель недостижим, это воображаемый объект.
дБи (dBi) характеризует коэффициент усиления антенны и ее направленные свойства по сравнению с изотропным излучателем. Строго говоря, если говорят, что данная антенна имеет коэффициент усиления, например, 8 дБ, то на самом деле имеется ввиду 8 дБи.
Может иметь только положительные значения.
дБм (dBm) — это децибелл по сравнению с «m», в данном случае по отношению к милливату. Иначе говоря, это значение того, на сколько децибелл данная мощность больше (или меньше) чем 1 мВт.
| дБ | P(изм)/P(оп) | дБ | P(изм)/P(оп) |
|---|---|---|---|
| 0 | 1 | 0,1 | 1,023 |
| -0,1 | 0,977 | 0,2 | 1,047 |
| -0,2 | 0,955 | 0,3 | 1,072 |
| -0,3 | 0,933 | 0,4 | 1,096 |
| -0,4 | 0,912 | 0,5 | 1,122 |
| -0,5 | 0,891 | 0,6 | 1,148 |
| -0,6 | 0,871 | 0,8 | 1,202 |
| -0,8 | 0,832 | 1 | 1,259 |
| -1 | 0,794 | 1,5 | 1,413 |
| -1,5 | 0,708 | 2 | 1,585 |
| -2 | 0,631 | 2,5 | 1,778 |
| -2,5 | 0,562 | 3 | 1,995 |
| -3 | 0,501 | 3,5 | 2,239 |
| -3,5 | 0,447 | 4 | 2,512 |
| -4 | 0,398 | 4,5 | 2,818 |
| -4,5 | 0,355 | 5 | 3,16 |
| -5 | 0,316 | 6 | 3,98 |
| -6 | 0,251 | 7 | 5,01 |
| -7 | 0,200 | 8 | 6,31 |
| -8 | 0,158 | 9 | 7,94 |
| -9 | 0,126 | 10 | 10 |
| -10 | 0,1 | 11 | 12,59 |
| -11 | 0,079 | 12 | 15,85 |
| -12 | 0,063 | 13 | 19,95 |
| -13 | 0,05 | 14 | 25,12 |
| -14 | 0,040 | 15 | 31,62 |
| -15 | 0,032 | 16 | 39,81 |
| -16 | 0,025 | 18 | 63,1 |
| -18 | 0,016 | 20 | 100 |
| -20 | 0,01 | 25 | 316 |
| -25 | 0,00316 | 27 | 501 |
| -30 | 0,001 | 30 | 1000 |
| -35 | 0,000316 | 35 | 3162 |
| -40 | 0,0001 | 40 | 10000 |
| -45 | 0,0000316 | 45 | 31623 |
| -50 | 0,00001 | 50 | 100000 |
| -60 | 0,000001 | 60 | 1000000 |
| -70 | 0,0000001 | 70 | 10000000 |
| -80 | 0,00000001 | 80 | 100000000 |
| -90 | 0,000000001 | 90 | 1000000000 |
| -100 | 0,0000000001 | 100 | 10000000000 |
Все это необходимо учитывать при выборе репитера сотовой связи. По всем вопросам по училению сотовой связи вы можете звонить нам по телефону, мы ответим на все Ваши вопросы.
Что такое децибел (дБ)? Перевод из децибел в разы.
Перевод из децибел в разы и обратно
Довольно часто в популярной радиотехнической литературе, в описании электронных схем употребляется единица измерения – децибел (дБ или dB).
При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (ёмкость, индуктивность, частоту).
Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт.
Тут всё понятно, есть электрический параметр или величина, которую нужно измерить. Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи.
Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?
Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.
Что такое децибел?
Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.
Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.
Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в логарифмическом масштабе.

График логарифмической зависимости
Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.
Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.
Причины для использования децибел всё-таки есть. Перечислим их.
 Частично ответ на этот вопрос кроется в так называемом законе Вебера-Фехнера. Это эмпирический психофизиологический закон, т.е основан он на результатах реальных, а не теоретических экспериментов. Суть его заключается в том, что любые изменения каких-либо величин (яркости, громкости, веса) ощущаются нами при условии, если эти изменения носят логарифмический характер.
Частично ответ на этот вопрос кроется в так называемом законе Вебера-Фехнера. Это эмпирический психофизиологический закон, т.е основан он на результатах реальных, а не теоретических экспериментов. Суть его заключается в том, что любые изменения каких-либо величин (яркости, громкости, веса) ощущаются нами при условии, если эти изменения носят логарифмический характер.

График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера
Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора, который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.

Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)
Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.
Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).
 Вторая причина широкого использования децибел является простота вычислений.
Вторая причина широкого использования децибел является простота вычислений.
Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.
Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.
Также децибелы очень удобны при графическом построении различных зависимостей. Все графики вроде диаграмм направленности антенн, амплитудно-частотных характеристик усилителей выполняют с применением децибел.
Децибел является безразмерной единицей измерения. Мы уже выяснили, что децибел на самом деле показывает, во сколько раз возросла, либо уменьшилась какая-либо величина (ток, напряжение, мощность). Отличие децибел от разов заключается лишь в том, что происходит измерение по логарифмическому масштабу. Чтобы это как-то обозначить и приписывают обозначение дБ. Так или иначе, при оценке приходится переходить от децибел к разам. Сравнивать с помощью децибел можно любые единицы измерения (не только ток, напряжение и проч.), так как децибел является относительной, безразмерной величиной.
Если указывается знак “-”, например, –1 дБ, то значение измеряемой величины, например, мощности, уменьшилось в 1,26 раз. Если перед децибелами не ставят никакого знака, то речь идёт об увеличении, росте величины. Это стоит учитывать. Иногда вместо знака “-” говорят о затуханиях, снижении коэффициента усиления.
Переход от децибел к разам.
На практике чаще всего приходится переходить от децибел к разам. Для этого есть простая формула:
Внимание! Данные формулы применяются для так называемых “энергетических” величин. Таких как энергия и мощность.
m = 10(n / 10) ,где m – отношение в разах, n – отношение в децибелах.
Например, 1дБ равен 10(1дБ / 10) = 1,258925…= 1,26 раза.
Аналогично,
Но, не всё так просто. Есть и подводные камни. Например, затухание сигнала составляет -10 дБ. Тогда:
при -10 дБ: 10(-10дБ / 10) = 0,1
Если мощность с 5 Вт уменьшилась до 0,5 Вт, то снижение мощности равно -10 дБ (уменьшению в 10 раз).
при -20 дБ: 10(-20дБ / 10) = 0,01
Здесь аналогично. При снижении мощности с 5 Вт до 0,05 Вт, в децибелах падение мощности составит -20 дБ (уменьшению в 100 раз).
Таким образом, при -10 дБ мощность сигнала уменьшилась в 10 раз! При этом если мы перемножим начальную величину сигнала на 0,1 ,то и получим значение мощности сигнала при затухании в -10 дБ. Именно поэтому значение 0,1 и указано без «разов», как в предыдущих примерах. Учитывайте эту особенность при подстановке в данные формулы значений децибел со знаком «-«.
Переход от разов к децибелам можно осуществить по следующей формуле:
n = 10 * log10(m) ,где n – значение в децибелах, m – отношение в разах.
Например, рост мощности в 4 раза будет соответствовать значению в 6,021 дБ.
10 * log10(4) = 6,021 дБ.
Внимание! Для пересчёта отношений таких величин как напряжение и сила тока существуют немного иные формулы:
(Сила тока и напряжение, это так называемые “силовые” величины. Поэтому и формулы отличаются.)
n – значение в децибелах, m – отношение в разах.
Если Вы успешно дошли до этих строк, то считайте, что сделали ещё один весомый шаг в освоении электроники!
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Учебное пособие по
децибел: дБ и дБм в сравнении с усилением и милливаттами
Понятие децибела (дБ) по понятным причинам сложно и сбивает с толку кого-то, кого только что представили.
к нему. Сочетание характеристик усиления, мощности и напряжения (и тока, но
не так часто), что для смешивания дБ, дБм, дБВт, ватт, милливатт, напряжения, милливольт и т. д. часто требуется
преобразование назад и вперед между линейными значениями и значениями децибел. Это краткое руководство поможет
пояснить разницу между работой с децибелами и линейными значениями.
Предупреждение о тревоге: использование децибел предполагает работу с логарифмами.
Логарифмы (бревна)
были впервые придуманы в начале 1600-х годов шотландским математиком.
Джон Напье, как инструмент для упрощения
операции умножения и деления путем их преобразования в более быстрые и менее подверженные ошибкам операции сложения и вычитания,
соответственно. это
стало возможным благодаря способу умножения двух чисел, выраженных как аналогичные базовые числа с
экспоненты могут быть получены путем простого сложения показателей вместе.Деление тех же чисел
выполняется вычитанием показателей степени. Это один из законов экспонент и выглядит так:
это:
На примере реальных чисел, где x = 10, a = 4, b = 1:
Закон экспонент работает для любого основного числа, а не только для 10. То есть:
Люди склонны делать меньше ошибок при сложении и вычитании чисел, поэтому преимущество логарифмов
очевидно.Помните, что логарифмы были разработаны до появления автоматических механических или электронных компьютеров.
были доступны. Логарифм использует свойства логарифмов для
расчет, но это отдельная крупная тема.
Это простые примеры, но они верны для любого основания или показателя степени. При отсутствии калькулятора в
Для того, чтобы быть полезным для общего применения, вам понадобится таблица чисел и их эквивалентных логарифмов.
Таблицы ранних журналов заполняли тома в зависимости от расстояния между числами (1.000,
1.001, 1.002, 1.003, по сравнению с 1.0, 1.1, 1.2, 1.3 и т. Д.). Хорошие новости для создателей
таблицы логарифмов
состоит в том, что требуется только одна декада чисел (например, от 1 до 10), поскольку
каждое предыдущее или последующее десятилетие является простым кратным степени 10.
Примечание. В этом обсуждении я использую основание 10, так как это основа нашей общей системы счисления.
термин «десятичный логарифм» для журналов по основанию 10. Вы могли слышать о
натуральные логарифмы, которые
использует базу e,
но e не очень часто используется при вычислении скалярных величин электрической мощности, напряжения и тока.
(хотя он используется, когда включены фазовые углы, т.е.е.,
Тождество Эйлера).
Натуральные логарифмы записываются как ln (x) без нижнего индекса ‘e’, тогда как обычно логарифмы с основанием 10
записываются просто как log (x) без нижнего индекса 10; т.е. не log e (x) или log 10 (x),
соответственно.
На базу = 10 журналов таблица:
журнал (100000) = 5,
журнал (10,000) = 4, журнал
(1000) = 3, журнал (10) = 1
Исключение и особый случай: журнал x (0) =
Не определено.Это так, потому что нет степени, в которую можно возвести любое число и получить 0 (ноль).
Вы можете асимптотически приближаться к нулю, но не можете достичь нуля. Никогда не будет числа ноль
отображается в логарифмической шкале; они обычно меняются от некоторой степени 10 до другой степени десяти. Пример
миллиметровой бумаги отображается справа. Он имеет 5 «циклов» или «десятилетий» диапазона. Обратите внимание, что нет
ноль по оси ординат.
Таким образом, десятичный (общий) логарифм числа — это показатель степени, до которого необходимо возвести 10, чтобы
чтобы получить это число.Другими словами, поскольку 10 в степени 2 равно 100 (10 2
= 100), логарифм по основанию 10 из 100 равен 2 (логарифм 10 100 = 2).
Это основной закон логарифмов:
журнал c (a) = b,
поэтому c b = a
Выполнение тех же операций умножения и деления, что и в верхней части страницы, с использованием фактических логарифмов:
10 000 * 10 = 100 000 и 10 000 ÷ 10
= 1 000
4 + 1 = 5 и 4-1 = 3
Это нормально, но в итоге вы получите логарифм искомого числа.Вопрос: кроме простого
например, как получить нужный ответ? Ответ: Посмотрите антилогарифм (антилог)
результат. В данном случае:
antilog 5 = 100000 и antilog 3 =
1 000
Более сложный и более вероятный пример с числами, не являющимися целыми степенями 10, может выглядеть примерно так:
x = 1,28 * 3,70 * 0,559 * 26,4
журнал (x) = журнал (1.28) + журнал (3,70) + журнал (0,559) + журнал (26,4)
журнал (x) = 0,1072 + 0,5682 + (-0,2526) + 1,4216 = 1,8444
Поскольку логарифм x
равно 1,8444, антилогарифм равен ‘x’, что составляет 69,9
Чек: x = 1,28 * 3,70 * 0,559 * 26,4 = 69,9
Я использовал свой калькулятор для поиска этих чисел в журналах и антиблогах, но до 1972 года, когда Hewlett Packard (HP)
представила свой научный
Калькулятор, среднестатистическому человеку без доступа к корпоративному или университетскому мэйнфрейму необходимо было использовать таблицу журналов для выполнения таких вычислений.
Кто вообще возьмется использовать логарифмы сегодня, спросите вы? Многие люди, в том числе и я, довольно часто при подсчете
каскадно
параметры системы, такие как коэффициент шума (NF) и точки пересечения (IP). Простое сложение и вычитание значений усиления в дБ и мощности в дБм не работает
с НФ и ИП.
В управляющих формулах используется умножение и деление значений линейного усиления и мощности, которые
требует сначала преобразовать дБ и / или дБм в линейные числа (коэффициент усиления и мВт) с помощью антиблокировок, выполняя каскадные вычисления,
а затем преобразование результата обратно в дБ и / или дБм с использованием журналов.
Не для всех каскадных операций системы требуется преобразование туда и обратно. Например, если только общая
требуется усиление системы и / или уровень выходной мощности, тогда расчеты могут быть выполнены либо с
линейные единицы (мВт и множители) или логарифмические единицы (дБм и дБ соответственно).
Определение «дБ» и «дБм»
Децибел (дБ) в электротехнике определяется как 10-кратный логарифм отношения по основанию 10.
между двумя уровнями мощности; е.г., P из / P в (другими словами, усиление). То есть:
N дБ = 10 * лог 10 (P1 / P2)
Следовательно, все усиления больше 1 выражаются как положительные децибелы (> 0), а усиление меньше
чем 1 выражаются в отрицательных децибелах (<0). Обратите внимание, что в случаях, с которыми сталкивается большинство из нас, линейный
отношение P1 / P2 должно быть положительным числом (> 0), поскольку логарифм 0 не определен и
логарифм отрицательных чисел являются комплексными (содержат как действительную, так и мнимую часть).ДБ
value, однако, теоретически может принимать любое значение от −∞ до + ∞, включая 0, что
— коэффициент усиления 1 [10 * log (1) = 0 дБ].
«дБм» — это единица мощности в децибелах, относящаяся к 1 мВт. Поскольку 0 дБ усиления
равна усилению 1,1 мВт, мощность на 0 дБ больше 1 мВт или 0 дБм.
Аналогично, единица мощности дБВт — децибелы относительно 1 Вт мощности.
1 мВт = 0 дБм
Соответственно, все значения дБм выше 0 больше 1 мВт, а все значения дБм меньше
0 меньше 1 мВт (см. Рис.1). Например, +3,01 дБм на 3,01 дБ больше, чем
1 мВт; то есть, или 0 дБм + 3,01 дБ = +3,01 дБм (2 мВт). −3,01 дБм равно 3,01 дБ
менее 1 мВт; то есть, или 0 дБм + (-3,01) дБ = -3,01 дБм (0,5 мВт).
В следующей таблице приведены некоторые числовые примеры, чтобы вы могли увидеть корреляцию между мВт и
дБм. Тот же набор значений, нанесенный на график в логарифмическом масштабе, даст прямую линию. Из-за логарифмической
отношения, график группирует меньшие значения против левой вертикальной оси.Увеличенная версия
диапазона от 0 до 1 мВт для ясности вставлена.
Рис. 1 — График мощности в дБм от мВт
Рис. 2 представляет собой таблицу и график отношения дБ к линейному усилению, аналогичный зависимости дБм от мВт на рис. 1. Примечание.
что числа и кривые точно такие же; изменяются только метки осей. Это потому, что дБм — это единица измерения
мощности, выраженной в дБ относительно 1 мВт (0 дБмВт).
Рис. 2 — График усиления в единицах дБмВт в зависимости отЛинейное отношение
Линейное усиление (соотношение выход / вход) в зависимости от логарифмического (децибелы, дБ) усиления
По сути, усиление — это коэффициент умножения (или деления). Например, усилитель может иметь
коэффициент усиления, который увеличивает сигнал в 4 раза (т. е. в 4 раза) от входа к выходу (см. рис. 3). Если
На усилитель подается сигнал 1 мВт (0 дБмВт), затем 1 мВт * 4 = 4 мВт
выходит. В децибелах коэффициент 4 эквивалентен 10 * log (4) = 6.02 дБ,
таким образом, 0 дБм плюс 6,02 дБ усиления дает +6,02 дБм на выходе.
1 мВт * 4
= 4 мВт
0 дБм + 6,02
дБ = 6,02 дБм
Рис. 3 — Коэффициент усиления одиночного усилителя.
Объединение коэффициентов усиления (линейных и дБ) с положительными значениями
Если усилитель с коэффициентом усиления 4 включен последовательно со вторым усилителем с коэффициентом усиления 6, то
общее усиление составляет 4 * 6 = 24. В децибелах коэффициент 6 эквивалентен 10 * log (6) = 7.78 дБ,
а коэффициент 24 эквивалентен 10 * log (24) = 13,8 дБ.
Так же, как 4 x 6 = 24 (линейное усиление), 6,02 дБ + 7,78 дБ = 13,8 дБ
(усиление в децибелах).
Если на усилитель подается сигнал 1 мВт (0 дБмВт), то из первого усилителя выходит 4 мВт,
и 24 мВт выходит из второго усилителя. См. Рис. 4.
1 мВт * 4
* 6 = 24 мВт
0 дБм + 6,02
дБ + 7,78 дБ = 13,8 дБм
Рис.4 — Двойной каскадный усилитель усиления.
Объединение усиления и потерь (линейных и дБ)
В следующем примере показано, что происходит при усилении <1 (потери), когда аттенюатор с коэффициентом усиления 1/6 размещается после первого усилителя вместо второго усилителя. Видеть Рис. 5.
4 * 1/6 = 2/3 (линейное усиление). Аналогично 6,02 дБ — 7,78 дБ = -1,76 дБ
(усиление в децибелах).
Как и в предыдущем примере, если сигнал 1 мВт (0 дБмВт) подается на усилитель с коэффициентом усиления
4, то выходит 4 мВт.Затем эти 4 мВт поступают в аттенюатор с линейным усилением 1/6
и выходит на уровне мощности 4/6 мВт (2/3 мВт).
Суммарное усиление в этом случае составляет 4/6 = 2/3, поэтому выходная мощность будет меньше, чем
входная мощность.
1 мВт * 4
* 1/6 = 2/3 мВт = 0,67 мВт
0 дБм + 6,02
дБ + (-7,78 дБ) = −1,76 дБм
Рис. 5 — Коэффициент усиления и аттенюатор каскадного усилителя.
Обратите внимание, что уровни мощности выше 0 дБм иногда включают знак «плюс» (+), чтобы
Подчеркните, что это не отрицательно.Это особенно верно, когда уровни мощности отображаются на блоке.
диаграмма, где присутствуют как положительные, так и отрицательные значения.
Сводка
При измерении мощности в лаборатории или в полевых условиях большинству людей проще добавить
и вычесть уровни усиления и мощности, чем умножить и разделить уровни усиления и мощности. Это возможно с помощью единиц дБ и дБм. Важный
следует помнить, что никогда не смешивайте линейный
единицы усиления (отношения) и единицы мощности (мВт) с логарифмическим усилением (дБ) и мощностью (дБм).
Величины должны быть либо в линейных единицах, либо в децибелах. Следующий тип расчета: НЕ
разрешено, потому что он смешивает линейные значения с логарифмическими значениями.
12 мВт + 34 мВт + 8 мВт + 20 дБ
Дополнительная информация о логарифмах
Логарифмы произведений
Свойство логарифмов, неявно использованное выше, утверждает следующее и является основанием для возможности
для сложения и вычитания значений логарифма вместо умножения их линейных эквивалентов.
журнал (h * j) = log (h) + log (j), а журнал (h / j) = log
(h) — журнал (j)
следовательно,
журнал (h * j / k * m / n) = log (h) + log (j) — log (k) + log (m) — log (n)
‘h * j / k * m / n’ может представлять каскад компонентов, которые имеют три устройства (h, j и m)
каждое с коэффициентом усиления> 1 и два устройства (k и n) каждое с коэффициентом усиления <1 (см. рис. 6). Общая система
усиление может быть вычислено либо путем умножения всех значений линейного усиления вместе, либо путем сложения всех децибел
вместе приобретать ценности.
Рис.6 — Каскадные компоненты
Подробнее о свойствах логарифмов
и свойства показателей.
Логарифмы экспонент
Следующее важно для понимания, почему коэффициент усиления мощности в терминах мощности равен
10 * log (P из / P в ) дБ, в то время как мощность прирост в терминах
напряжения составляет 20 * log (В на выходе / В на ) дБ.
журнал (c f ) = f * log (c),
, потому что c f равно c, умноженному на себя ‘f’ раз. Например, если f
= 4:
c f = c 4
= с * с * с * с
журнал (c 4 ) = журнал (c * c * c * c) = журнал (c) + журнал (c) + журнал
(c) + журнал (c) = 4 * журнал (c) .
Коэффициент усиления по мощности в зависимости от коэффициента усиления по напряжению
Прирост мощности составляет P на выходе / P на , а усиление по напряжению составляет V на выходе / V на .
Коэффициент усиления мощности на основе отношения мощностей в децибелах определяется как 10 * log (P из / P в ). Мощность
коэффициент усиления по напряжению составляет [(В на выходе 2 / R) / (В на выходе 2 / R)],
поскольку по закону Ома P = V 2 / R.Буква R в знаменателях сокращается, оставляя V из 2 / V из 2 ,
что равно (V из / V из ) 2 , как определено правилом экспонент
это говорит
a c / b c = (a / b) c . Следовательно:
10 * журнал = 10 * 2 * журнал = 20 *
журнал
Важное примечание: Напряжение усиление по напряжению составляет 10 * log (В на выходе / В на ) дБ,
то же, что и с мощностью прирост в пересчете на мощности .Это только при мощности прирост
выражается через напряжение , что 20 * log (В на выходе / В на ) дБ
уравнение применяется. Это обычная путаница.
Прирост <1 (убыток) в отрицательных децибелах
Никакая математическая операция не является произвольной, поэтому потеря мощности сигнала (коэффициент усиления <1) отображается как отрицательное значение и, следовательно, вычитается при каскадном вычислении. Это простой демонстрация, но достойна упоминания.
журнал (1 / f) = журнал (1) — журнал (f) = 0 — журнал (f) = -log (f)
Пожалуйста, отправляйте любые комментарии или исправления по адресу
.
Опубликовано: 18 октября, 2016
.
дБм в телекоммуникационных приложениях и преобразование единиц измерения: «дБм» в «мВт»
Что такое «дБм»?
дБмВт (иногда дБмВт или децибел-милливатт) — это сокращение для отношения мощностей в децибелах (дБ) измеренной мощности к одному милливатту (мВт). Он используется в радио-, микроволновых и волоконно-оптических сетях в качестве удобного средства измерения абсолютной мощности из-за его способности выражать как очень большие, так и очень маленькие значения в краткой форме. Сравните дБВт, который относится к одному ватту (1000 мВт).
Поскольку это ватт, это абсолютная единица измерения абсолютной мощности. Для сравнения: децибел (дБ) — это безразмерная единица, используемая для количественной оценки отношения между двумя значениями, например отношения сигнал / шум.
В аудио и телефонии дБм обычно указывается относительно импеданса 600 Ом, в то время как при работе с радиочастотой дБм обычно указывается относительно импеданса 50 Ом.
Преобразование единиц: «дБм» в «мВт»
Уровень мощности 0 дБмВт соответствует мощности 1 милливатт.Увеличение уровня на 3 дБ приблизительно эквивалентно удвоению мощности, что означает, что уровень 3 дБмВт примерно соответствует мощности 2 мВт. Для каждого уменьшения уровня на 3 дБ мощность уменьшается примерно наполовину, в результате чего –3 дБмВт соответствует мощности примерно 0,5 мВт.
Чтобы выразить произвольную мощность P в мВт как x в дБм, или наоборот, можно использовать следующие эквивалентные выражения:
где P — мощность в Вт, а x — уровень мощности в дБмВт. Ниже представлена таблица с полезными кейсами:
дБм: стандартный отраслевой прибор
Интенсивность сигнала (мощность на единицу площади) может быть преобразована в мощность принятого сигнала путем умножения на квадрат длины волны и деления на 4π (см. «Потери на трассе в свободном пространстве»).
В практике Министерства обороны США обычно понимается невзвешенное измерение, применимое к определенной полосе пропускания, которая должна быть указана или подразумевается.
В европейской практике псофометрическое взвешивание может быть, как указано в контексте, эквивалентным dBm0p, что является предпочтительным.
В аудиосистеме 0 дБмВт часто соответствует приблизительно 0,775 В, поскольку 0,775 В рассеивает 1 мВт при нагрузке 600 Ом. [6] Меры дБ против этого опорного напряжения без ограничения 600 Ом.И наоборот, для ВЧ-ситуаций с нагрузкой 50 Ом 0 дБмВт соответствует приблизительно 0,224 В, поскольку 0,224 В рассеивает 1 мВт при нагрузке 50 Ом.
дБм не является частью Международной системы единиц и поэтому не рекомендуется использовать в документах или системах, которые придерживаются единиц СИ (соответствующей единицей СИ является ватт). Однако прямой децибел (дБ), являющийся безразмерным отношением двух чисел, вполне приемлем.
Выражение в дБм обычно используется для измерений оптической и электрической мощности, но не для других типов мощности (например, тепловой).Доступен список уровней мощности в ваттах, который включает множество примеров, не обязательно связанных с электрической или оптической мощностью.
дБм был впервые предложен в качестве отраслевого стандарта в документе «Новый стандартный индикатор громкости и эталонный уровень».
.
Решено: В чем разница между db, dbi и dbm?
•
Желательно: —
децибел — Если приемник очень чувствителен к радиочастотным сигналам, он может принимать сигналы мощностью всего 0,000000001 Вт.
• Логарифм — это показатель степени, до которого нужно возвести число 10, чтобы достичь некоторого заданного значения. Если нам дать число 1000 и попросить найти логарифм (log), мы обнаружим, что log 1000 = 3, потому что 10 ^ 3 = 1000.Обратите внимание, что наш логарифм 3 — это показатель степени. В отношении логарифмов важно отметить, что логарифм отрицательного числа или нуля не существует.
• Журнал (-100) = undefined!
• Журнал (0) = undefined!
• Децибелы — это относительная единица измерения, в отличие от абсолютного измерения в милливаттах.
дБм: —
• 1 мВт = 0 дБм
• Значение м в дБм означает просто тот факт, что эталонный сигнал составляет 1 милливатт (1 мВт) и, следовательно, измерение дБм измерение абсолютной мощности.
• Соотношение между шкалой децибел и шкалой ватт можно оценить, используя следующие практические правила:
• +3 дБ удвоит значение ватт:
• (10 мВт + 3 дБ ≈ 20 мВт)
• Аналогично, -3 дБ уменьшит значение ватт вдвое:
• (100 мВт — 3 дБ ≈ 50 мВт)
• +10 дБ увеличит значение ватт в десять раз :
• (10 мВт + 10 дБ ≈ 100 мВт)
• И наоборот, -10 дБ снизит значение ватт до одной десятой этого значения:
• (300 мВт — 10 дБ ≈ 30 мВт )
дБи: —
• Единица измерения дБи относится только к усилению антенны.«I» означает «изотропный», что означает, что изменение мощности относится к изотропному излучателю.
• Изотропный излучатель — это теоретический идеальный передатчик, который производит полезное электромагнитное поле во всех направлениях с одинаковой интенсивностью и со 100-процентной эффективностью в трехмерном пространстве. Одним из примеров изотропного радиатора является солнце.
Спасибо,
Посмотреть решение в исходном сообщении
.
дБн дБFS дБВ в вольт преобразование звука цифровой — калькулятор вольт в дБн и дБВ дБ мВт УЗД дБ децибел 0 дБFS — преобразование дБ вольт нормальные децибелы объяснение взаимосвязи абсолютный уровень аналогового звука истинный среднеквадратичный преобразователь преобразователь децибел в преобразователь dbfs расчет коэффициента затухания онлайн соотношение эталонное звуковое оборудование звукозапись dBFS dBVU 0 дБ преобразователь уровня логарифма звука от амплитуды до пика импеданса напряжение для профессионального потребления аудио цифровой аналоговый уровень записи
дБ дБн дБFS дБВ в вольт преобразование звука цифровой — калькулятор вольт в дБн и дБВ дБ мВт SPL дБ децибел 0 dBFS — преобразование дБ вольт нормальные децибелы объяснение взаимосвязи аналоговый аудио абсолютный уровень преобразователь истинного среднеквадратичного значения преобразователь преобразователя децибел в dbfs расчет онлайн-коэффициент потерь затухания коэффициент усиления эталонная аудиотехника запись звука dBFS dBVU 0 дБ преобразователь логарифма звука от пика до пика импеданс напряжения для профессионального аудио цифровой аналоговый уровень записи — sengpielaudio Se ngpiel Берлин
Заполните серое поле выше и щелкните соответствующую полосу «вычислить» под ним.p-p = от пика до пика.
Эталонное напряжение для 0 дБн составляет 0,775 В (0,77459667 В), а для 0 дБВ — ровно 1,0 В.
Прокрутите вниз, чтобы найти формулы для напряжения и мощности и расчет абсолютного уровня.
| Происхождение индекса dBu происходит от «u = un loaded», а dBV происходит от «V = 1 вольт». Некоторые говорят: «u» в дБн означает, что полное сопротивление нагрузки равно и , и с оконечной нагрузкой и, вероятно, будет высоким. Что такое дБу? Логарифмическое отношение напряжения со ссылкой напряжения от В 0 = 0.7746 вольта ≡ 0 дБ |
Шкала: Уровень в дБн и дБВ по сравнению с напряжением в В
| Уровень дБн | Напряжение В | Уровень дБВ | |
| Международная студия | +4 ● | 1.228 | +1,78 |
| Стандартный уровень 1 В | +2,22 | 1 | 0 исх. |
| Стандартный уровень 0,775 В | 0 исх. | 0,775 | -2,22 |
| Внутренний уровень | -7,78 | 0,316 | −10 ● |
| Разница уровней между студийным уровнем +4 дБн и -10 дБВ потребительским уровнем составляет Δ L = 11.78 дБ (12 дБ). Разница уровней между уровнем dBu и уровнем dBV составляет Δ L = 2,2 дБ. Преобразование уровня L (дБу) в напряжение (вольт) составляет В = 0,775 × 10 ( L /200006 ) . |
| Все полевые величины, такие как напряжение или звуковое давление, являются всегда истинными среднеквадратичными значениями, если не указано иное. В математике среднеквадратичное значение (сокращенно RMS |
| Для синусодиальных напряжений или токов с омической нагрузкой вычисления можно упростить с помощью RMS = амплитуда / √2 |
| Уровень | Напряжение |
| Примечание — Сравнение дБ SPL и дБА: формулы преобразования для измеренных значений дБА в уровень звукового давления дБУЗД и наоборот не существует. Также нельзя преобразовать «дБА в вольты» и наоборот. Преобразование возможно только для измерения одной отдельной частоты. |
| Pro аудиооборудование часто указывает спецификации шума по шкале А — не , потому что он хорошо коррелирует с нашим слухом, а потому, что может «скрыть» неприятные компоненты гула, которые создают плохие характеристики шума. Слова для светлых умов: Всегда задавайтесь вопросом, что скрывает производитель |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Объяснение: Что такое «dBFS»? (Цифровое аудио)
dBFS — Уровень цифровой записи
| Аналоговые и цифровые уровни — это разные области. |
♦ Часто задаваемый вопрос: «Пожалуйста, помогите мне конвертировать из dBFS в dBu».
Никогда не выражайте уровни аналогового сигнала через dBFS.
Следуйте этому, и вы никого не запутаете.
| Нет преобразователя децибел в dBFS Уведомление — Сравнение dBu и dBFS: на самом деле нет фиксированного мирового стандарта , например, −20 дБFS = +4 дБн = 0 дБVU. Цифровая шкала пиков не эквивалентна аналоговой шкале RMS. Вы не можете сопоставить dBFS и dBu. |
| dBu — это вольт — вы измеряете его вольтметром. Аналоговый аудиосигнал: положительное и отрицательное напряжение. dBFS, напротив, двоичное число. |
| Пиковое напряжение не существует. *) Неправильно указывать уровни пикового напряжения в дБн. |
*) http://www.rane.com/note169.html
*) http://www.rane.com/pdf/ranenotes/No_Such_Thing_as_Peak_Volts_dBu.pdf
dBFS должен иметь в начале знак минус. Нет чего-то вроде +6 dBFS.
| Такой стандартизированной ссылки нет. x dBFS — это цифровой уровень напряжения (пиковое), а y dBVU или dBu — аналоговый уровень напряжения (RMS). Цифровой и аналоговый — две совершенно разные области. Вот почему нет никакой связи между dBFS и dBVU или dBu вообще. Совет: Наблюдайте только за своими цифровыми индикаторами и поднимайтесь до 0 dBFS, но никогда не превышайте Никогда не принимайте следующую забавную игру в догадки как должное. Используйте его только в качестве приблизительного ориентира: Спецификация BBC: −18 дБFS = PPM «4» = 0 дБн • EBU R68-2000 — Европейский вещательный союз рекомендует: цифровой уровень У вещательных компаний EBU есть проблема, потому что они хотят использовать старые медленные измерители со шкалой |
| Примечание. Рекомендации EBU по установке максимального усиления на –9 дБ dBFS не должны применяться, если они не работают для Европейского вещательного союза . У которых максимальные уровни цифровых мастеров компакт-дисков равны −9dBFS, не должны удивляться, если компакт-диски недостаточно громкие. 9 дБ до верха остаются свободными и бесполезны. |
| LUFS = Единицы громкости относительно полной шкалы |
Формулы для напряжения и мощности
и расчет абсолютного уровня
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
дБм указывает, что эталонная мощность составляет P 0 = 1 милливатт = 0.001 Вт ≡ 0 дБ
Преобразование отношений напряжения или мощности в децибелы дБ — таблица и диаграмма
Таблица уровней звукового давления и соответствующих значений звукового давления и интенсивности звука
среднеквадратичное напряжение , пиковое напряжение и пиковое размах напряжения
Параметры формы синусоидального сигнала сети или «мощности» приведены в таблице ниже:
| Среднее напряжение | RMS напряжение ( В RMS ) | Пиковое напряжение ( В p ) = ( Û ) | Пиковое напряжение ( В pp ) |
| 0 вольт | 117 В = В RMS = ~ В | 165 В = √2 × В RMS = 0,5 × В pp | 330 В = 2 × √2 × В RMS = 2 × В p |
| 0 вольт | 230 В = В RMS = ~ В | 325 В = √2 × В RMS = 0,5 × В pp | 650 В = 2 × √2 × В RMS = 2 × В p |
| Значение В RMS переменного напряжения В (t) = В 0 × f (t) определяется так, чтобы эффективная мощность постоянного тока соответствовала В RMS 2 / R = V RMS × I RMS до омического сопротивления средней резистивной мощности этого переменного напряжения до того же сопротивления. |
Пик-фактор означает отношение пикового напряжения к среднеквадратичному напряжению.
Если вам нужно рассчитать аттенюатор (расчет затухания), вы рассчитаете делитель напряжения .
Преобразователи напряжения
| Напряжение | В СКЗ = ~ В | В стр | V pp |
| Среднее значение напряжения (СКЗ) В СКЗ = | – | 0.7071 × В p | 0,3535 × В pp |
| Пиковое напряжение В p = | 1,414 × В RMS | – | 0,5000 × В pp |
| Пиковое напряжение В pp = | 2,828 × В RMS | 2.000 × В стр. | – |
Различные уровни напряжения
| Уровень | Уровень L в дБ | Действующее значение напряжения | Напряжение от пика до пика |
| Европейский студийный уровень — уровень вещания ARD | +6 дБн | 1.55 В | 4,38 В |
| Международный студийный уровень — США | +4 дБн | 1,228 В | 3,47 В |
| Внутренний учет (потребительские единицы) | −10 дБВ | 0,3162 В ≡ −7,78 дБн | 0,894 В |
| Уровень звукового давления (слуховой порог) | 0 дБ | 2 × 10 −5 Па ≡ 0 дБSPL | 5,66 × 10 −5 Па |
| Reference studio level re 0.775 вольт | 0 дБн | 0,7746 В | 2,19 В |
| Эталонный уровень студии re 1 вольт | 0 дБВ | 1,0000 В | 2,828 В |
Международные справочные значения
| Физическая единица | Единица уровня | Справочное значение | Примечание |
| Напряжение | В 0 = 0.775 В | ≡ 0 дБн | Аудиотехника, без определения импеданса! |
| Напряжение | В 0 = 1 В | ≡ 0 дБВ | Аудиотехника, США |
| Напряжение | В 0 = 1 × 10 −6 В | ВЧ приемник и усилитель техники | |
| Напряжение | В 0 = 0,224 В | ВЧ технология — опорный сигнал 1 мВт при Z = 50 Ом | |
| Напряжение | В = 1.228 В | Студийный уровень +4 дБн, США — эталонный 0,7746 В | |
| Напряжение | В = 1,55 В | Студийный уровень +6 дБн, ARD — эталонный 0,7746 В | |
| Напряжение | В = 0,3162 В | Уровень домашней записи −10 дБВ — эталонный 1,0 В −7,78 дБн | |
| Звуковое давление | p 0 = 2 × 10 −5 Па | ≡ 0 дБ | Уровень звукового давления SPL, слуховой порог (звук , размер поля ) |
| Скорость звуковых частиц | v 0 = 5 × 10 −8 м / с | ≡ 0 дБ | |
| Интенсивность звука | I 0 = 1 × 10 −12 Вт / м 2 | ≡ 0 дБ | Порог боли при 1 Вт / м 2 (Звук энергия размер) |
| Мощность | P 0 = 1 Вт | ≡ 0 дБВт | Необходимо всегда указывать эталонный импеданс |
| Мощность | P 0 = 1 мВт | ≡ 0 дБм | Z = 600 Ом (телефоны) или Z = 50 Ом (антенны) |
| Напряженность электрического поля | E 0 = 1 × 10 −6 В / м |
| Децибелы (дБ) Калькулятор Децибелы определяются как десятикратный логарифм отношения мощностей.Децибелы преобразуют Этот калькулятор выполняет преобразование между децибелами, коэффициентом усиления напряжения (или тока) и коэффициентом усиления мощности. Уравнения: Уровень в дБ: L = 20 × log ( В 1 / В 2 ) = 10 × log ( P 1 / P 2 ) |
| дБм — это логарифмическая мера мощности по сравнению с 1 мВт, , что означает, что она зависит от мощности. Его можно преобразовать в напряжение, если известно полное сопротивление нагрузки. Обычно полное сопротивление (нагрузка) составляет 600 Ом. Уравнение: Уровень в дБм: L P = 10 × log ( P / 0,001) |
| Простое практическое правило: при работе с мощностью: 3 дБ — это дважды, 10 дБ — 10 раз. При работе с напряжением или током: 6 дБ — дважды, 20 дБ — 10 раз. |
| Почему ширина полосы и частота среза находятся на уровне «–3 дБ»? Почему мы всегда уменьшаем усиление фильтра на 3 дБ? Полная ширина на полувысоте (FWHM). Ответ: Это точка, в которой энергия (мощность) падает до значения ½ или 0,5 = 50 процентов от начальной мощности в виде количества энергии , что эквивалентно (-) 3 дБ = 10 × log (0,5) . Падение мощности (-) 3 дБ — это уменьшение на 50% до значения 50%. Здесь напряжение падает до значения √ (½) или 0,7071 = 70,71 процента от начального напряжения в качестве величины поля, эквивалентной (-) 3 дБ = 20 × log (0,7071). Падение напряжения (-) 3 дБ — это уменьшение на 29,29% до значения 70.71%. |
| (-) 3 дБ означает ½ электроэнергии, и, поскольку мощность пропорциональна квадрату напряжения , значение будет 0,7071 или 70,71% от напряжения полосы пропускания. √½ = 1 / √2 = √0,5 = 0,7071. P ~ В 2 , то есть 0,5 ~ 0,7071 2 . |
| Звукорежиссеры и звукорежиссеры («слуховые люди») в основном используют обычное (звуковое) количество полей . Вот почему они говорят: Частота среза устройства (микрофон, усилитель, громкоговоритель) — это частота, при которой уровень выходного напряжения уменьшается до значения (-) на 3 дБ ниже уровня входного напряжения (0 дБ). ). ● (-) 3 дБ соответствует коэффициенту √½ = 1 / √2 = 0,7071, что составляет 70,71% от входного напряжения. Акустикам и звукооператорам («шумоподавителям»), кажется, больше нравится (звук) количество энергии . Нам говорят: |
| Примечание: Коэффициент усиления мощности (усиление мощности) не является распространенным в аудиотехнике. Даже усилители мощности для громкоговорителей не усиливают мощность. Они усиливают звуковое напряжение, которое перемещает звуковую катушку. |
| Примечание: Величина звукового поля (звуковое давление p , электрическое напряжение В ) не является величиной звуковой энергии (интенсивность звука I , мощность звука P ak ). I ~ p 2 или P ~ V 2 . Иногда можно услышать утверждение: Частота среза находится там, где уровень L уменьшается на (-) 3 дБ. Все, что пользователь хочет сказать нам с такой точностью: уровень равен уровню или дБ равен дБ. |
.

