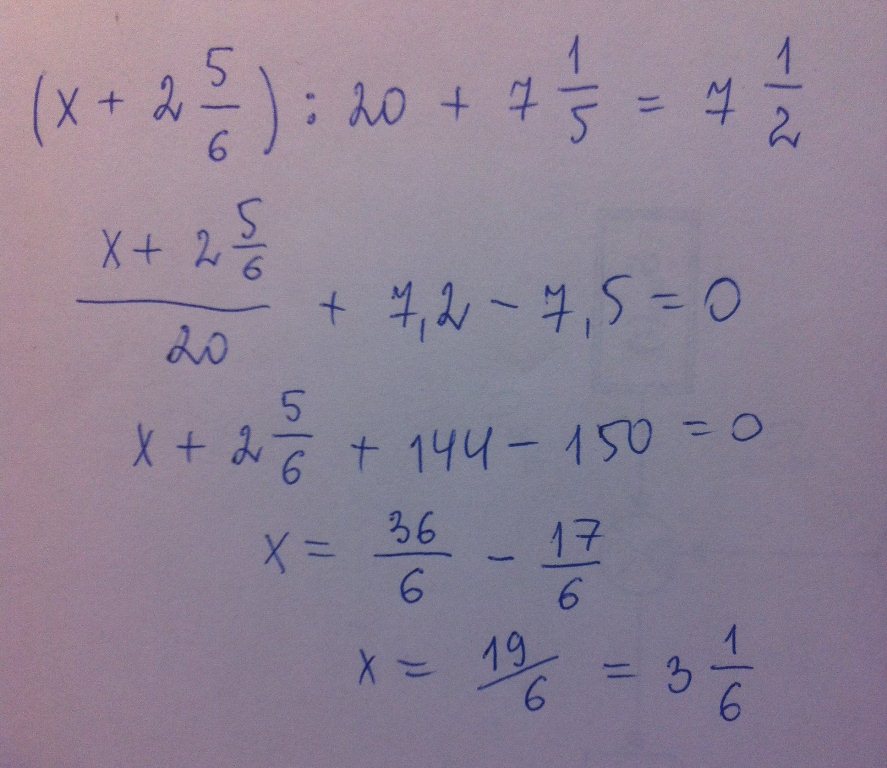X 2 х: Решите уравнение x^2=-2 (х в квадрате равно минус 2)
11.3.4. Решение показательных уравнений, приводящихся к квадратным уравнениям.
Многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax2+bx+c=0.
Примеры.
Решить уравнение:
1) 4x+2x+1-3=0. Представим 4x в виде степени с основанием 2.
(22)x+2x∙21-3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:
(2x)2+2∙2x-3=0;
вводим новую переменную: пусть 2x=y;
y2+2y-3=0.
Дискриминант для четного второго коэффициента: D1=12-1∙(-3)=1+3=4=22 – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
y1+y2=-2, y1∙y2=-3. Подбираем корни: y1=-3, y2=1.
Возвращаемся к переменной х:
1) 2x=-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).
2) 2x=1. Число 1 можно представлять в виде нулевой степени по любому основанию.
2x=20;
x=0.
Ответ: 0.
2) 0,252x-5∙0,52x+4=0. Решаем аналогично. Представляем 0,252x— в виде степени с основанием 0,5.
(0,52)2x-5∙0,52x+4=0;
(0,52x)2-5∙0,52x+4=0.
0,52x=y; ввели новую переменную у и получили приведенное квадратное уравнение:
y2—5y+4=0;
Дискриминант D=b2-4ac=52-4∙1∙4=25-16=9=32 — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
y1+y2=5, y1+y2=4. Корни приведенного квадратного уравнения находим подбором: y1=1, y2=4 и возвращаемся к переменной х:
1) 0,52x=1; число 1 можно представлять в виде нулевой степени по любому основанию.
0,52x=0,50;
2x=0;
x=0.
2) 0,52x=4; приведем степень 0,52x к основанию 2, применив формулу: (1/a)x =а-х
(1/2)2x=22;
2-2x=22; приравниваем показатели:
— 2x=2 |:(-2)
x=-1.
Ответ: -1; 0.
Представим левую и правую части в виде степеней с основанием 4, используя формулы: а-х=1/ax и ax∙ay=ax+y .
Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.
Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Решение простых показательных уравнений
Простые примеры на показательные уравнения позволят овладеть методикой их решения. Задания не слишком сложные и будут полезными для всех кто изучает показательные уравнения, готовится к тестированию, контрольным или вступительным экзаменам.
Пример 1. Решить уравнение (0,5)х =.
Решение: Первое что нужно сделать это свести уравнение к одному основанию. С этой целью преобразуем правую сторону показательного уравнения
В итоге уравнение сведется к виду
Теперь основы ровны, поэтому можем приравнять показатели
и найти ответ x=-2,5.
Вот такие простые вычисления.
Пример 2. Решить уравнение (2/3)х*(9/8)х =27/64.
Решение: Преобразим правую и левую сторону показательного уравнения к одной основе
Подставим в уравнение и приравняем показатели
Таким простым методом нашли решение показательного уравнения x=3.
Пример 3. Решить уравнение 52х-7х-35*52х+35*7х=0.
Решение: Сгруппируем слагаемые, содержащие 52х и 7х.
Последняя запись показательного уравнения многих заводит в тупик. (Не всем легко найти ответ).
Тогда, давайте перепишем уравнение в виде
Согласно свойствам показательных функций решение равно нулю x=0. Только возведением к 0 степени можно получить единицу.
Для наглядности посмотрите графики показательных функций. Они пересекаются в точке x=0.
Пример 4. Решить уравнение 14х+2+5*14х-1=2749.
Решение: В подобных задачах необходимо вынести основу с наименьшим показателем. Для этого распишем уравнение к виду
Получили что решение равно единице.
Пример 5. Решить уравнение (0,6)х+2 =25/9 .
Решение: Такого рода задачи следует решать по следующей схеме.
Обязательно превратить число 0,6 к дробному виду
Далее уже поступают исходя из условия, в нашем случае превращаем правую сторону.
Приравниваем показатели, предварительно изменив знак в каком либо, чтобы получить одинаковую основу
x+2=-2; x=-2-2=-4.
Решение показательного уравнения x=-4.
Пример 6. Решить уравнение (0,25)х-1=2*sqrt(2)
Решение: Преобразим показательное уравнение к одной основе
Подставим выражение в уравнение
Решение уравнения равно 1/4.
Пример 7. Решить уравнение (1,44)х-4=6/5.
Решение: Не сразу можно догадаться как упрощать уравнения.
Распишем сначала правую сторону 6/5=1,2.
Основу в показателе сводим к виду
После подстановки приравниваем показатели при одинаковых основаниях
2(x-4)=1; 2x-8=1; 2x=9;x=9/2=4,5.
Решения уравнения x=4,5.
Пример 8. Решить уравнение
Решение: Используем основополагающее правило для показательных уравнений — свести уравнение к слагаемым с одинаковым основанием.
Выполним манипуляции с основой
Подставляем в уравнение и приравниваем степени
Решение показательного уравнения равно x=-2.
Пример 9. Решить уравнение 3х-1+3х-2+3х-3=13.
Решение: Расписываем слагаемые так, чтобы потом сгруппировать слагаемые с одинаковим показником
Дальнейшие действия достаточно просты
Уравнение удавлетваряет значение x=3.
Пример 10. Найти сумму решений уравнения
Решение: Можно догадаться что придется вычислять квадратное уравнение.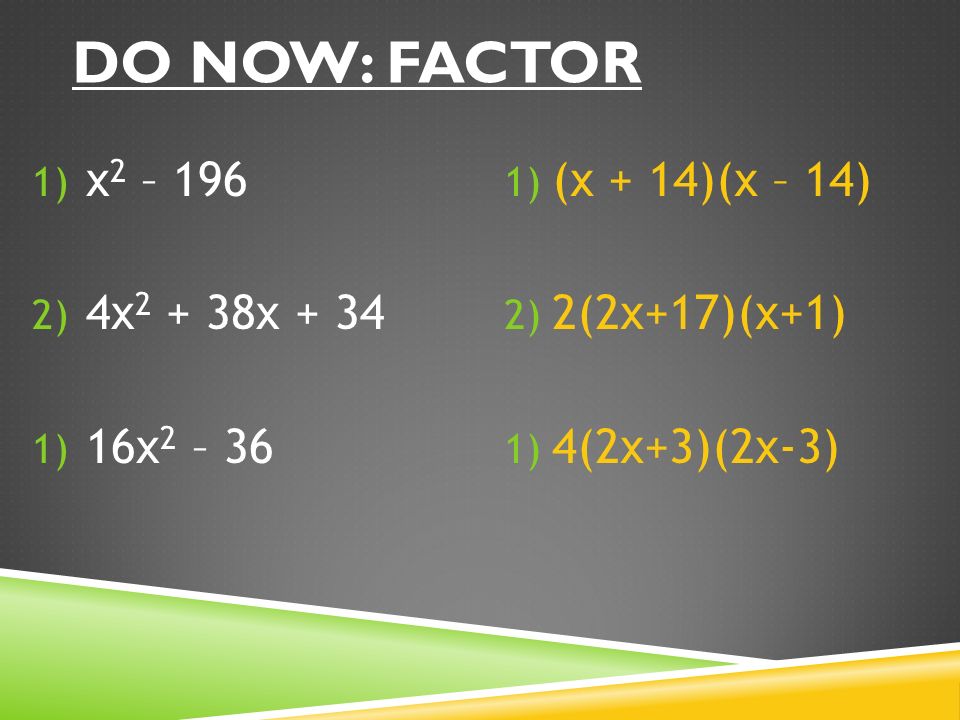 Но к нему еще нужно прийти. Для начала запишем 0,6 в виде
Но к нему еще нужно прийти. Для начала запишем 0,6 в виде
Подставим в показательное уравнения
Теперь можно приравнять степени при основаниях
Корни уровнения x=0; x=-1/2.
Их сумма равна
0-1/2=-0,5.
На этом знакомство с возможными примерами простых показательных уравнений завершено. Сложные примеры можно найти на страницах сайта. Оставайтесь с нами и мы подготовим Вас лучше репетиторов.
Похожие материалы:
Урок 12. решение алгебраических уравнений разложением на множители — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №12. Решение алгебраических уравнений разложением на множители.
Перечень вопросов, рассматриваемых в теме
1) типы алгебраических уравнений;
2) решение алгебраические уравнения методом разложения на множители;
3) методы решения алгебраических уравнений.
Глоссарий по теме
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Симметрическим уравнением 3-ей степени называют уравнение вида: ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что такое алгебраическое уравнение?
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над полем F.
Степенью алгебраического уравнения называют степень многочлена P.
Например, уравнение
является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.
Связанные определения. Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Примеры и разбор решения заданий тренировочного модуля
- Алгебраические уравнения, решаемые разложением на множители:
Пример 1.
x3 – 3x – 2 = 0.
Решение: I способ
D(–2) : ,
Можно догадаться, что число х1 = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.
(х + 1)( х2 –х–2) = 0;
х + 1 = 0 или х2 –х–2 = 0;
х1 = –1 х2,3 = ;
х2,3 = ;
х2 = –1, х3 = 2
Ответ: –1; 2.
II способ
x3 + х2 – х2 – х – 2x – 2 = 0;
(x3 + х2) – (х2 + х) – 2(x + 1) = 0;
х2(х + 1) – х(х + 1) – 2(х + 1) = 0;
(х + 1) (х2 –х–2) = 0;
(х + 1) (х + 1) (х –2) = 0;
(х –2) = 0;
х1 = –1, х2 = 2
Ответ: –1; 2.
- Уравнения, сводящиеся к алгебраическим
- Биквадратные уравнения
На прошлом уроке мы познакомились с данным видом уравнений
Определение. Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Метод решения
Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х2.
Новое квадратное уравнение относительно переменной у: ay2+by+c=0.
Решая это уравнение, мы получаем корни квадратного уравнения
y1 и y2.
Решая эти два уравнения (y1=x12 и y2=x12) относительно переменной x, мы получаем корни данного биквадратного уравнения.
Порядок действий при решении биквадратных уравнений
- Ввести новую переменную у=х2
- Подставить данную переменную в исходное уравнение
- Решить квадратное уравнение относительно новой переменной
- После нахождения корней (y1; y2) подставить их в нашу переменную у=х2 и найти исходные корни биквадратного уравнения
Пример 2.
х4 – 8х2 – 9 = 0.
Решение: Пусть у = х2, где у 0; у2 – 8у – 9 = 0;
По формулам Виета:
у1 = –1; у2 = 9;
Первое решение отбрасываем ( у 0),
а из второго находим х1 = –3; х2 = 3.
Ответ: х1 = –3; х2 = 3.
2 Симметрические уравнения
Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.
Симметрическим уравнением 3-ей степени называют уравнение вида ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:
10. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.
(х + 1)(ах2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах2 + (b – а)x + а = 0,
первое уравнение и доказывает интересующее нас утверждение.
20. У симметрического уравнения корней, равных нулю, нет.
30. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.
Пример 3.
х3 + 2x2 + 2х + 1 = 0.
Решение: У исходного уравнения обязательно есть корень х = –1.
Разлагая далее левую часть на множители, получим
(х + 1)(x2 + х + 1) = 0.
Квадратное уравнение
x2 + х + 1 = 0 не имеет корней.
Ответ: –1.
2 Возвратные уравнения
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Рассмотрим возвратное уравнение четвёртой степени вида
ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.
Порядок действий при решении возвратных уравнений вида ax4 + bx3 + cx2 + bx + a = 0:
- разделить левую и правую части уравнения на .
 При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения; - группировкой привести полученное уравнение к виду
- ввести новую переменную , тогда выполнено
, то есть ;
в новых переменных рассматриваемое уравнение является квадратным: at2 +bt+c–2a=0;
- решить его относительно t, возвратиться к исходной переменной.
Пример 4
2x4 – 3x3 – 7x2 –15x + 50 = 0.
Решение: Разделим на x2, получим:
Введем замену:
Пусть
тогда 2t2 – 3t – 27 = 0
t=-3 x2+3x+5=0 D<0 | 2×2-9x+10=0 x=2; x=2,5 |
Ответ: .
Уравнения в целых числах (диофантовы уравнения) / math5school.ru
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями
Решениями
такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому
уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма.
Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в
целых числах – великая теорема Ферма: уравнение
xn + yn = zn
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых
числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы
Поэтому следует для разных типов уравнений выбирать собственные методы
решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод остатков;
метод бесконечного спуска.
Задачи с решениями
1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.
Решение
Запишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
б) 5х + 7у = 19;
в) 201х – 1999у = 12.
Решение
а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в
целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
x0 = 1, y0 = 2.
Тогда
5x0 + 7y0 = 19,
откуда
5(х – x0) + 7(у – y0) = 0,
5(х – x0) = –7(у – y0).
Поскольку числа 5 и 7 взаимно простые, то
х – x0 = 7k, у – y0 = –5k.
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x3 + y3 = 3333333;
б) x3 + y3 = 4(x2y + xy2 + 1).
Решение
а) Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x3 + y3
может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7
дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
4. Решить
а) в простых числах уравнение х2 – 7х – 144 = у2 – 25у;
б) в целых числах уравнение x + y = x2 – xy + y2.
Решение
а) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
2 х 16, 2 у 16.
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x2 – (y + 1)x + y2 – y = 0.
Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из
исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x2 + y2 + z2 = x3 +
y3 + z3 ?
Решение
Попробуем подбирать такие тройки, где у = –z. Тогда y3 и z3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь
вид
x2 + 2y2 = x3
или, иначе,
x2(x–1) = 2y2.
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно
много, а именно, это все числа вида 2n2+1. Подставляя в x2(x–1) = 2y2 такое число, после несложных преобразований
получаем:
y = xn = n(2n2+1) = 2n3+n.
Все тройки, полученные таким образом, имеют вид (2n2+1; 2n3+n; –2n3– n).
Ответ: существует.
6. Найдите такие целые числа x, y, z, u, что x2 + y2 + z2 + u2 = 2xyzu.
Решение
Число x2 + y2 + z2 + u2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x2 + y2 + z2 + u2 делится на 4, но при этом 2xyzu не делится
на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x2 + y2 + z2 + u2 не делится на 4, а 2xyzu делится на 4 –
опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
x = 2x1, y = 2y1, z = 2z1, u = 2u1,
и исходное уравнение примет вид
x12 + y12 + z12 + u12 =
8x1y1z1u1.
Теперь заметим, что (2k + 1)2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1,
z1, u1 нечётны, то x12 + y12 + z12 +
u12 не делится на 8. А если ровно два из этих чисел нечётно, то x12 + y12 +
z12 + u12 не делится даже на 4. Значит,
x1 = 2x2, y1 = 2y2, z1 = 2z2, u1 =
2u2,
и мы получаем уравнение
x22 + y22 + z22 + u22 =
32x2y2z2u2.
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
Ответ: (0; 0; 0; 0).
7. Докажите, что уравнение
(х – у)3 + (y – z)3 + (z – x)3 = 30
не имеет решений в целых числах.
Решение
Воспользуемся следующим тождеством:
(х – у)3 + (y – z)3 + (z – x)3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
abc = 10.
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5,
либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в
целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у2.
Решение
Очевидно, что
если х = 1, то у2 = 1,
если х = 3, то у2 = 9.
Этим случаям соответствуют следующие пары чисел:
х1 = 1, у1 = 1;
х2 = 1, у2 = –1;
х3 = 3, у3 = 3;
х4 = 3, у4 = –3.
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a3 – b3 – c3 = 3abc, a2 = 2(b + c).
Решение
Так как
3abc > 0, то a3 > b3 + c3;
таким образом имеем
b
Складывая эти неравенства, получим, что
b + c
С учётом последнего неравенства, из второго уравнения системы получаем, что
a2
Но второе уравнение системы также показывает, что а – чётное число. Таким образом, а = 2, b = c = 1.
Таким образом, а = 2, b = c = 1.
Ответ: (2; 1; 1)
10. Найти все пары целых чисел х и у, удовлетворяющих уравнению х2 + х = у4 + у3 + у2 + у.
Решение
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у2 + 1),
или
х(х + 1) = (у2 + у)(у2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому,
приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
х1 = 0, у1 = 0;
х2 = 0, у2 = –1;
х3 = –1, у3 = 0;
х4 = –1, у4 = –1.
Произведение (у2 + у)(у2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля,
только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих
Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих
исходному уравнению:
х5 = 5, у5 = 2;
х6 = –6, у6 = 2.
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
а) ху = х + у + 3;
б) х2 + у2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х3 + 21у2 + 5 = 0;
б) 15х2 – 7у2 = 9.
3. Решить в натуральных числах уравнение:
а) 2х + 1 = у2;
б) 3·2х + 1 = у2.
4. Доказать, что уравнение х3 + 3у3 + 9z3 = 9xyz в рациональных числах имеет единственное решение
x = y = z = 0.
5. Доказать, что уравнение х2 + 5 = у3 в целых числах не имеет решений.
Bell X-2
Проведя первую серию испытаний самолетов Х-1 специалисты
фирмы «Белл» в 1949 году начали проектирование
нового ракетного самолета Х-2 для исследований аэро- и термодинамических явлений на скоростях с
числом М~3. Им помогали их коллеги из Национального координационного комитета по
авиации NACA и ВВС США. Предполагалось, что постепенно, по мере модернизации, Х-2 сможет
достигнуть высоты в 60 километров. На корпусе самолета, выполненном из нержавеющей стали, были
установлены приборы для сбора информации о влиянии нагрева на конструкционные материалы.
Первый опытный образец Х-2 был построен в 1952 году. Как обычно, сначала в июне 1952 были
выполнены несколько планирующих полетов со специально приспособленного самолета-носителя
Boeing В-50 и облет с работающим двигателем. Однако
вторая попытка полета с запуском двигателя привела к катастрофе. 12 мая 1953 года во время
заправки Х-2, который находился еще в бомбоотсеке В-50, экспериментальный самолет взорвался.
X-2 был сброшен и сгорел в воздухе. От взрыва погибли летчик-испытатель фирмы Bell Jean Ziegler и Frank Wolko — член экипажа
самолета-носителя EB-50A, находившиеся в бомбовом отсеке.
После этого испытания были прерваны до конца 1955 года, когда был готов второй экземпляр
Х-2. Его первый полет с работающим двигателем состоялся 18 ноября 1955 года. В июле следующего
была достигнута рекордная скорость в горизонтальном полете (3360 км/ч), а 7 сентября -
высота 38430 м. Во время следующего вылета 27 сентября 1956 г., достигнув рекордной скорости 3,2М,
которая не была превышена до 1961 г., самолет потерпел катастрофу, а пилот капитан Милбурн Г. Апт погиб.
Потеря самолёта, который оценивался в 3 млн долларов, прервала исследования, проводимые ВВС США и NASA с помощью экспериментальных самолётов в области больших скоростей и высот полёта. Причины катастрофы выяснить не удалось.
Х-2 представляет собой моноплан классической схемы с низкорасположенным стреловидным ( ~ 40 гр) крылом, имеющим острую переднюю кромку. Крыло оснащено носовыми щитками, расположенными приблизительно на 2/5 длины передней кромки, а также обычными элеронами, снабженными триммерами. Стабилизатор — стреловидный, управляемый, а киль — прямой, с рулем направления. Фюзеляж (длиной около 12 м) в центральной части имеет форму, близкую к цилиндрической, а передняя и хвостовая части-конусообразную. На верхней и нижней поверхностям фюзеляжа находятся два больших продольных обтекателя, которые закрывают коммуникации и оборудование системы управления, а также выпускаемую во время приземления лыжу (в первом опытном образце). Крыло и оперение выполнены из нержавеющей стали, а фюзеляж — из легированной молибдено-никелевой стали. Поскольку Х-2 стартует в воздухе с оборудованного соответствующим образом бомбардировщика Boeing В-50, шасси Х-2 предназначено лишь для посадки и рассчитано на небольшие нагрузки. У первого экземпляра самолета шасси состояло из одноколесной передней стойки и лыжи, выполняющей роль колеса главного шасси. Во втором опытном экземпляре использовались уже две лыжи, которые при необходимости убирались в крыло.
Крыло оснащено носовыми щитками, расположенными приблизительно на 2/5 длины передней кромки, а также обычными элеронами, снабженными триммерами. Стабилизатор — стреловидный, управляемый, а киль — прямой, с рулем направления. Фюзеляж (длиной около 12 м) в центральной части имеет форму, близкую к цилиндрической, а передняя и хвостовая части-конусообразную. На верхней и нижней поверхностям фюзеляжа находятся два больших продольных обтекателя, которые закрывают коммуникации и оборудование системы управления, а также выпускаемую во время приземления лыжу (в первом опытном образце). Крыло и оперение выполнены из нержавеющей стали, а фюзеляж — из легированной молибдено-никелевой стали. Поскольку Х-2 стартует в воздухе с оборудованного соответствующим образом бомбардировщика Boeing В-50, шасси Х-2 предназначено лишь для посадки и рассчитано на небольшие нагрузки. У первого экземпляра самолета шасси состояло из одноколесной передней стойки и лыжи, выполняющей роль колеса главного шасси. Во втором опытном экземпляре использовались уже две лыжи, которые при необходимости убирались в крыло.
Предназначение самолета для полетов на больших скоростях и высотах потребовало разработки безотказного и безопасного способа катапультирования пилота в случае аварии. В своем выборе конструкторы остановились на варианте отделения всей кабины от самолета. Кабина имела теплоизоляционное покрытие и стационарное переднее остекление, состоящее из двух стекол. Стекла не только сохраняли свои свойства до температуры 540 oС, но и поглощали инфракрасные лучи. В целях уменьшения солнечного нагрева конструкции и увеличения интенсивности теплоотвода в окружающую среду самолет покрашен в белый цвет.
В самолете использован восьмикамерный ракетный двигатель XLR-25-CW-1 фирмы Curtiss-Wright с максимальной тягой ~71,10 кН. Двигатель был оснащен насосами для подачи топлива (этиловый спирт и жидкий кислород), а также оборудованием для запуска, выключения и регулирования тяги двигателя во время полета. Емкость топливных баков обеспечивала работу двигателя в течение 2,3-6,0 мин.
| Описание | |
|---|---|
| Разработчик | Bell |
| Обозначение | X-2 |
| Тип | Экспериментальный самолет |
| Экипаж, чел. | 1 |
| Геометрические и массовые характеристики | |
| Длина самолета, м | 13, 41 |
| Высота самолета, м | 4,13 |
| Размах крыла, м | 9,76 |
| Площадь крыла, м2 | 24,30 |
| Максимальная взлетная масса, кг | 13000 (11300) |
| Масса пустого самолета, кг | 7300-8200 |
| Удельная нагрузка на крыло, кг/м2 | 535 |
| Силовая установка | |
| Число двигателей | 1 |
| Двигатель | ЖРД Curtiss-Wright XLR-25-CW-1 |
| Тяга двигателя, кгс | 6804 (7250) |
| Тяговооруженность | 0,54 |
| Время работы двигателя, мин | |
| Масса топлива | |
| Летные данные | |
| Максимальная скорость полета на высоте, км/ч | 3360 |
| Максимальное число Маха | 3 (3,2) |
| Динамический потолок, м | 38430 |
Источники информации:
- «Энциклопедия вооружений» / «Кирилл и Мефодий», 1998 — CD-ROM /
- Vojenska latadla / Vaclav Nemecek, 1982
- Фотогалерея NASA
ESX X-TWO — 2-х канальные / Усилители / По компонентам
Описание модели
ESX X-TWO:
Серия Xenium, 2-х канальный усилитель, RMS 2 х 100Вт @ 4 Ом
Информация о
ESX X-TWO:
Немецкая компания ESX предлагает вашему вниманию семейство компактных усилителей под названием Xenium. В этой линейке представлены три модели – двухканальный X-Two, четырехканальный X-Four и моноблок X-One. Каждый из этих усилителей участвовал в тестах известных европейских журналов car audio, и каждый неизменно получал наивысшие оценки экспертов.
В этой линейке представлены три модели – двухканальный X-Two, четырехканальный X-Four и моноблок X-One. Каждый из этих усилителей участвовал в тестах известных европейских журналов car audio, и каждый неизменно получал наивысшие оценки экспертов.
Первое, что бросается в глаза при взгляде на усилители Xenium, это их сверхмалые размеры – 200 х 51 х 260 мм, одинаковые для всех трех моделей. Благодаря этому, их монтаж может быть произведен «стопкой» друг на друга. Корпус усилителей отделан покрытием под «рояльный лак», а логотип фирмы на верхней поверхности при включении аппарата подсвечивается. Еще одним немаловажным отличием от подобных моделей продающихся на рынке является то, что многоканальные модели работают в «музыкальном» классе А/В (моноблок в классе D), имея при этом солидную мощность. Монтаж комплектующих выполнен по технологии SMD, что обеспечивает высокие надежность и качество изготовления устройства.
Усилители имеют достойное оснащение – регулируемые фильтра ВЧ/НЧ с возможностью включения режима «бэндпасс», схема подъема баса, в моноблоке предусмотрен фильтр «сабсоник» и вход для дистанционного регулятора уровня (поставляется в комплекте). Во всех моделях предусмотрена тройная система защиты – от перегрева, перегрузки и, что встречается крайне редко даже в гораздо более дорогих усилителях, защита от неправильного подключения питания (переполюсовки). Моноблок работает с нагрузкой до 1 Ом, выдавая при этом 750 Вт, и имеет возможность подключения второго такого же с целью удвоения выходной мощности при работе на один сабвуфер, что делает его уникальным учитывая его стоимость, оснащение и размеры.
Во всех моделях предусмотрена тройная система защиты – от перегрева, перегрузки и, что встречается крайне редко даже в гораздо более дорогих усилителях, защита от неправильного подключения питания (переполюсовки). Моноблок работает с нагрузкой до 1 Ом, выдавая при этом 750 Вт, и имеет возможность подключения второго такого же с целью удвоения выходной мощности при работе на один сабвуфер, что делает его уникальным учитывая его стоимость, оснащение и размеры.
Подытоживая вышесказанное и учитывая сравнительно невысокую цену при отличном качестве звучания, можно смело сказать, что усилители ESX Xenium являются одними из лучших в своем классе и станут превосходным выбором для использования в вашей аудиосистеме.
Основные особенности и характеристики:
— сверхкомпактные размеры
— возможность монтажа «стопкой»
— отделка под «рояльный лак»
— логотип с подсветкой
— многоканальники класса А/В
— моноблок класса D
— фильтра ВЧ/НЧ/бэндпасс
— дистанционный регулятор баса (для моноблока)
— возможность включения 2-х моноблоков в режиме master/slave
— защита от переполюсовки, перегрева, перегрузки
Характеристики
ESX X-TWO:
| Название | Значение |
|---|---|
| Входы/Выходы | |
| Количество каналов усилителя | 2 |
| Линейные входы | 1 пара RCA |
| Мощность | |
| Выходная мощность на нагрузку 2 Ом | 2 х 175 Вт |
| Выходная мощность на нагрузку 4 Ом | 2 х 100 Вт |
| Выходная мощность при мостовом включении на нагрузку 4 Ом | 1 х 350 Вт |
| Общие | |
| Габаритные размеры (ШхВхГ) | 200 х 51 х 260/270 мм |
| Питание | |
| Предохранитель | 2 х 20 А |
| Технические характеристики | |
| Входная чувствительность | 200 — 6000 мВ |
| Входное сопротивление | 47 кОм |
| Коэффициент демпфирования | >300 |
| Коэффициент нелинейных искажений |
|
| Максимальная мощность | 1 х 700 Вт |
| Отношение сигнал/шум | >104 дБ |
| Разделение каналов | 74 дБ |
| Фильтры | |
| Частота ФВЧ | 15 — 250 Гц |
| Частота ФНЧ | 30 — 250 Гц |
| Функции и особенности | |
| Выносной регулятор уровня | Нет |
| Класс усиления | AB |
| Эквалайзер НЧ (Bass Boost) | 0 — 12 дБ на 45 Гц |
0.
 047UF 280VAC, 0.047мкф х 280в 10% Class X2 конденсатор полипропиленовый помехоподавляющий 18x5x1
047UF 280VAC, 0.047мкф х 280в 10% Class X2 конденсатор полипропиленовый помехоподавляющий 18x5x1
Описание
конденсаторы помехоподавляющие
Металлизированные полипропиленовые плёночные конденсаторы класса Х2 предназначены для подавления электромагнитных помех, возникающих в сети в процессе работы импульсных источников питания, сварочного оборудования, мощных генераторов, силовых коммутационных ключей, мощных реле и других промышленных электротехнических устройств.
Конденсаторы серии MPX класса X2 имеют конструкцию с металлизированным пленочным полипропиленовым диэлектриком. Медные радиальные выводы покрыты плакированной сталью. Конденсаторы герметизированы в пластмассовом корпусе эпоксидной смолой. Конденсаторы отличаются хорошими свойствами самовосстановления, небольшими габаритными размерами, высокой емкостью, малыми потерями и высокой надежностью. Используются в светодиодном освещении, энергосберегающих лампах, система поджига, блоках зарядки, контроллерах, измерительных приборах, телекоммуникационном оборудовании и др.
Класс X2 выдерживает пиковые напряжения до 2.5 кВ, которые могут быть вызваны молнией или коммутационными процессами в соседнем оборудовании и в самом устройстве, где используется конденсатор и применяются в приложениях, где неисправность конденсатора не приведет к опасному удару электрическим током.
Технические характеристики
Диапазон номинальной емкости: 0.022…1 мкФ
Рабочее напряжение: 280 В перем.тока, 50/60 Гц
Напряжение диэлектрической прочности: 4.3*280 В пост.тока
Погрешность емкости: 10%
Тангенс угла потерь: менее 0.001
Сопротивление изоляции: более 15000 МОм
Диапазон рабочих температур: -40…85оС
Технические параметры
| Класс | X2 |
| Номинальное переменное напряжение (50/60 Гц) Uac,В | 280 |
| Емкость | 0.047 |
| Единица измерения | мкф |
| Класс | X2 |
| Номинальное переменное напряжение (50/60 Гц) Uac,В | 280 |
| Емкость | 47 |
| номинал | нФ |
| Допуск номинальной емкости,% | 10 |
| Серия | X2-MKP |
| Диэлектрик | Полипропилен(MKP) |
| Корпус | прямоугольный |
| Выводы | радиальные проволочные |
| Длина корпуса L,мм | 18 |
| Диаметр(ширина) корпуса D(W),мм | 10 |
| Толщина корпуса T,мм | 4 |
| Расстояние между выводами F,мм | 15 |
| Рабочая температура,С | -40. ..85 ..85 |
Дополнительная информация
Калькулятор емкостей
2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)
Калькулятор алгебры — это калькулятор, который дает пошаговую помощь по задачам алгебры.
Посмотреть другие примеры »
Заявление об отказе от ответственности:
Этот калькулятор не идеален. Пожалуйста, используйте на свой страх и риск и сообщите нам, если что-то не работает. Спасибо.
Как пользоваться калькулятором
Введите задачу по алгебре в текстовое поле.
Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14.
Попробуйте этот пример прямо сейчас! »
Другие примеры
Примеряем примеры на
Примеры
страница — это самый быстрый способ научиться пользоваться калькулятором.
(Показатель: «в степень»)
sqrt (квадратный корень) (пример: sqrt (9))
Другие математические символы
Учебное пособие
Прочтите полное руководство, чтобы узнать, как построить графики уравнений и проверить свое домашнее задание по алгебре.Учебное пособие по калькулятору
»
Мобильное приложение
Загрузите мобильное приложение MathPapa! Работает офлайн!
Обратная связь
(Для студентов 13+)
Пожалуйста, используйте эту форму обратной связи, чтобы отправить свой отзыв. Спасибо!
Нужно больше практических задач?
Попробуйте MathPapa
Математическая практика
Заполнение калькулятора квадратов
Использование калькулятора
Этот калькулятор является
решатель квадратных уравнений , который решит полиномиальное уравнение второго порядка в форме ax 2 + bx + c = 0 для x, где a 0, используя
, завершив квадратный метод . 2 — 6x + \ dfrac {7} {2} = 0 \)
2 — 6x + \ dfrac {7} {2} = 0 \)
Теперь продолжите решать это квадратное уравнение, выполнив метод квадратов.2 = 4 \)
Извлечь квадратный корень из обеих частей
\ (x = \ pm \ sqrt [] {4} \)
, следовательно,
\ (х = + 2 \)
\ (х = — 2 \)
экспонентов: основные правила | Purplemath
Purplemath
Экспоненты — это сокращение от многократного умножения одного и того же самого на себя.Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 3 . «Степень», равная 3 в этом примере, означает, сколько раз умножается значение. То, что умножается (в этом примере 5), называется «базой».
Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 3 » произносится как «пять в третьей степени» или «пять в третьей степени».
MathHelp.com
Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе».Итак, «5 3 » обычно произносится как «пять кубов».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы лучше будем иметь дело с «27», чем с «3 3 ». Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « xxxxxx ».
Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « xxxxxx ».
У экспонентов есть несколько правил, которые мы можем использовать для упрощения выражений.
Чтобы упростить это, я могу думать о том, что означают эти показатели.«До третьего» означает «умножение трех копий», а «до четвертого» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме. Сначала я расширяюсь:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
Теперь я могу убрать скобки и сложить все множители:
( xxx ) ( xxxx ) = xxxxxxx
Это семь копий переменной. «Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
xxxxxxx = x 7
Собираем все вместе, шаги следующие:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
= xxxxxxx
= x 7
Тогда упрощенная форма ( x 3 ) ( x 4 ) будет:
Обратите внимание, что x 7 также равно x (3 + 4) .Это демонстрирует первое основное правило экспоненты:
Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты:
( x м ) ( x n ) = x (m + n)
Однако мы НЕ можем упростить ( x 4 ) ( y 3 ), потому что базы разные: ( x 4 ) ( y 3 ) = xxxxyyy = ( x 4 ) ( y 3 ). Ничего не сочетается.
Ничего не сочетается.
Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом:
( a 5 b 3 ) ( a b 7 ) = ( a 5 ) ( a ) ( b 3 ) ( б 7 )
Теперь я хочу добавить мощности на a и b .Однако у второго и , похоже, нет мощности. Что мне добавить для этого срока?
Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:
( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( a 5 ) ( a 1 ) ( b 3 ) ( b 7 )
Теперь могу комбинировать:
( a 5 ) ( a 1 ) ( b 3 ) ( b 7 ) = a 5 + 1 b 3 + 7 = a 6 b 10
Если сложить все вместе, моя ручная работа будет выглядеть так:
( a 5 b 3 ) ( a b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) =
В следующем примере есть две силы, одна из которых в некотором смысле находится «внутри» другой.
Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, указанного в скобках. В этом случае база четвертой степени равна x 2 . Умножение четырех копий этой базы дает мне:
Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как:
( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( xx ) ( xx ) ( xx ) ( xx )
Убрав круглые скобки, получим:
( xx ) ( xx ) ( xx ) ( xx ) = xxxxxxxx
Это строка из восьми копий переменной. «Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
xxxxxxxx = x 8
Собираем все вместе:
( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 )
= ( xx ) ( xx ) ( xx ) ( xx )
= xxxxxxxx
= х 8
Обратите внимание, что ( x 2 ) 4 = x 8 , и что 2 × 4 = 8.Это демонстрирует правило второй степени:
Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:
Если у вас есть продукт в круглых скобках и сила в скобках, то сила идет на каждый элемент внутри. Например:
Например:
( xy 2 ) 3 = ( xy 2 ) ( xy 2 ) ( xy 2 )
= ( xxx ) ( y 2 y 2 y 2 )
= ( xxx ) ( yyyyyy )
= x 3 y 6
= ( x ) 3 ( y 2 ) 3
Другой пример:
Предупреждение: это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению.
Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильный. На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.
На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.
Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) 2 , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому:
( x — 2) 2 = ( x — 2) ( x — 2)
= x ( x — 2) — 2 ( x — 2)
= xx — 2 x — 2 x + 4
= x 2 — 4 x + 4.
Ошибка в виде ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается сделать все в своей голове, вместо того, чтобы показать свою работу.Делайте все аккуратно, и вы вряд ли совершите эту ошибку.
Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что у c внутри скобок это «в степени 1».)
(Мне нужно помнить, что у c внутри скобок это «в степени 1».)
( a 2 ) 4 ( b 3 ) 4 ( c 1 ) 4
= ( a 2 × 4 ) ( b 3 × 4 ) ( c 1 × 4 )
= a 8 b 12 c 4
Партнер
Есть еще одно правило, которое может или не может быть рассмотрено в вашем классе на данном этапе:
Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе).
Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:
Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:
Упростить [(3
x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0
Кого волнует эта фигня в квадратных скобках? Я уверен, что нет, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха!
[(3 x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0 = 1
Между прочим, как только ваш класс охватывает «до нуля», вы должны ожидать упражнения, подобного приведенному выше, на следующем тесте. Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с помощью экспонент. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество рабочих примеров.)
Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.
URL: https://www.purplemath.com/modules/exponent.htm
Ввод математических задач на этом сайте
Быстро! Мне нужна помощь с:
Выберите пункт справки по математике. ..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombinations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, факторы наибольшего общего, наименьшее число общих фракций, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочлены, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок
..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombinations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, факторы наибольшего общего, наименьшее число общих фракций, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочлены, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок
Три правила экспонент — Полный курс алгебры
Урок 13, Раздел 2
Вернуться в раздел 1
Правило 1. Та же база
Та же база
Правило 2. Мощность продукта
Правило 3. Мощность мощности
Правило 1. То же основание
«Чтобы умножить степени одного основания, сложите экспоненты».
Например, a 2 a 3 = a 5 .
Почему мы добавляем экспоненты? Из-за того, что означают символы. Секция 1.
Пример 1. Умножение 3 x 2 · 4 x 5 · 2 x
Решение . Задача означает (Урок 5): умножьте числа, затем сложите степени x :
3 x 2 · 4 x 5 · 2 x = 24 x 8
Два фактора x — x 2 — умножить на пять факторов x — x 5 — умножить на один фактор x , произвести всего 2 + 5 + 1 = 8 факторов x : x 8 .
Задача 1. Умножить. Примените правило Same Base.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| а) | 5 x 2 · 6 x 4 = 30 x 6 | б) | 7 x 3 · 8 x 6 = 56 x 9 | ||||
| c) | x · 5 x 4 = 5 x 5 | г) | 2 x · 3 x · 4 x = 24 x 3 | ||||
| e) | x 3 · 3 x 2 · 5 x = 15 x 6 | е) | x 5 · 6 x 8 y 2 = 6 x 13 y 2 | ||||
| г) | 4 x · y · 5 x 2 · y 3 = 20 x 3 y 4 | ч) | 2 x y · 9 x 3 y 5 = 18 x 4 y 6 | ||||
| i) | a 2 b 3 a 3 b 4 = a 5 b 7 | к) | a 2 до н. Э. 3 b 2 ac = a 3 b 3 c 4 Э. 3 b 2 ac = a 3 b 3 c 4 | ||||
| к) | x м y n x p y q = x m + p y n + q | л) | a p b q ab = a p + 1 b q + 1 | ||||
Проблема 2.Различают следующие:
x · x и x + x .
x · x = x ². x + x = 2 x .
Пример 2. Сравните следующее:
а) x · x 5 б) 2 · 2 5
Решение .
а) x · x 5 = x 6
б) 2 · 2 5 = 2 6
Часть b) имеет ту же форму , что и часть a). Это часть а) с x = 2.
Один множитель 2 умножает пять множителей 2, давая шесть множителей 2.
2 · 2 = 4 здесь неверно.
Проблема 3. Примените правило Same Base.
| а) | x x 7 = x 8 | б) | 3 · 3 7 = 3 8 | в) | 2 · 2 4 · 2 5 = 2 10 | ||
| г) | 10 · 10 5 = 10 6 | д) | 3 x · 3 6 x 6 = 3 7 x 7 | ||||
Проблема 4. Примените правило Same Base.
Примените правило Same Base.
| а) | x n x 2 = x n + 2 | б) | x n x = x n + 1 | ||||
| c) | x n x n = x 2 n | г) | x n x 1 — n = x | ||||
| e) | x · 2 x n — 1 = 2 x n | е) | x n x m = x n + m | ||||
| г) | x 2 n x 2 — n = x n + 2 | ||||||
Правило 2: Сила произведения факторов
«Увеличьте каждый коэффициент до той же степени. «
«
Например, ( ab ) 3 = a 3 b 3 .
Почему мы можем это сделать? Опять же, согласно значению символов:
( ab ) 3 = ab · ab · ab = aaabbb = a 3 b 3 .
Порядок факторов не имеет значения:
ab · ab · ab = aaabbb .
Задача 5. Применить правила экспонент.
| а) | ( x y ) 4 = x 4 y 4 | б) | ( pqr ) 5 = p 5 q 5 r 5 | в) | (2 abc ) 3 = 2 3 a 3 b 3 c 3 |
| d) x 3 y 2 z 4 ( xyz ) 5 | = | x 3 y 2 z 4 · x 5 y 5 z 5 Правило 2. |
| = | x 8 y 7 z 9 То же основание. | |
Правило 3: Мощность мощности
«Чтобы взять степень степени, умножьте экспонент».
Например, ( a 2 ) 3 = a 2 · 3 = a 6 .
Почему мы это делаем? Опять же, из-за того, что означают символы:
( a 2 ) 3 = a 2 a 2 a 2 = a 3 · 2 = a 6
Задача 6. Примените правила экспонент.
| а) | ( x 2 ) 5 = x 10 | б) | ( a 4 ) 8 = a 32 | в) | (10 7 ) 9 = 10 63 |
Пример 3. Примените правила экспонент: (2 x 3 y 4 ) 5
Примените правила экспонент: (2 x 3 y 4 ) 5
Решение . В скобках указаны три фактора: 2, x 3 и y 4 . Согласно Правилу 2 мы должны брать пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,
(2 x 3 y 4 ) 5 = 2 5 x 15 y 20
Проблема 7.Применяйте правила экспонент.
| а) | (10 a 3 ) 4 = 10 000 a 12 | б) | (3 x 6 ) 2 = 9 x 12 | |
| c) | (2 a 2 b 3 ) 5 = 32 a 10 b 15 | г) | ( xy 3 z 5 ) 2 = x 2 y 6 z 10 | |
| e) | (5 x 2 y 4 ) 3 = 125 x 6 y 12 | е) | (2 a 4 до н. Э. 8 ) 6 = 64 a 24 b 6 c 48 Э. 8 ) 6 = 64 a 24 b 6 c 48 | |
Проблема 8.Применяйте правила экспонент.
a) 2 x 5 y 4 (2 x 3 y 6 ) 5 = 2 x 5 y 4 · 2 5 x 15 y 30 = 2 6 x 20 y 34
b) abc 9 ( a 2 b 3 c 4 ) 8
= abc 9 · a 16 b 24 c 32 = a 17 b 25 c 41
Проблема 9.Используйте правила экспонент, чтобы вычислить следующее.
а) (2 · 10) 4 = 2 4 · 10 4 = 16 · 10 000 = 160 000
б) (4 · 10 2 ) 3
= 4 3 · 10 6 = 64 000 000
в) (9 · 10 4 ) 2
= 81 · 10 8 = 8100000000
В степенях 10 столько же нулей, сколько в экспоненте 10.
Пример 4. Квадрат x 4 .
Решение . ( x 4 ) 2 = x 8 .
Чтобы возвести в квадрат степень, удвойте экспоненту.
Проблема 10. Возведите следующее.
| а) | x 5 = x 10 | б) | 8 a 3 b 6 = 64 a 6 b 12 | |
| c) | −6 x 7 = 36 x 14 | г) | x n = x 2 n | |
Часть c) иллюстрации: Квадрат числа никогда не бывает отрицательным.
(−6) (- 6) = +36. Правило знаков.
Задача 11. Примените правило экспонент — если возможно.
| а) | x 2 x 5 = x 7 , Правило 1. | б) | ( x 2 ) 5 = x 10 , Правило 3. |
| в) | x 2 + x 5 |
| Невозможно. Правила экспонент применяют только к умножению. |
В итоге: Добавьте показателей степени, когда одно и то же основание появляется дважды: x 2 x 4 = x 6 . Умножьте экспоненты, когда основание появится один раз — и в скобках:
( x 2 ) 5 = x 10 .
Задача 12. Примените правила экспонент.
| а) | ( x n ) n = x n · n = x n 2 | б) | ( x n ) 2 = x 2 n |
Проблема 13. Примените правило экспонент или добавьте похожие термины — если возможно.
Примените правило экспонент или добавьте похожие термины — если возможно.
а) 2 x 2 + 3 x 4
Невозможно. Это не похоже на термины .
б) 2 x 2 · 3 x 4 = 6 x 6 . Правило 1.
в) 2 x 3 + 3 x 3
= 5 x 3 .Как термины. Показатель степени не меняется.
г) x 2 + y 2
Невозможно. Это не термины.
д) x 2 + x 2
= 2 x 2 . Как термины.
е) x 2 · x 2
= x 4 . Правило 1
г) x 2 · y 3
Невозможно.Разные базы.
ч) 2 · 2 6
= 2 7 . Правило 1
i) 3 5 + 3 5 + 3 5 =
3 · 3 5 (При добавлении подобных терминов) = 3 6 .
Мы продолжим правила экспонентов в 21 уроке.
Следующий урок: Умножение. Распределительное правило.
Вернуться в раздел 1
Содержание | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Математическая сцена — Уравнения III — Урок 3
Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения
| 2008 Rasmus ehf и Jhann sak | Уравнения III |
Урок
3
Пересечение
точек графиков
Как начать поиск точек, в которых два графика
y = f (x) и y = g (x) пересекаются?
Мы уже знаем, как найти график
f (x) пересекает ось x.Здесь y = 0. Мы вычисляем его, решая
уравнение f (x) = 0.
Когда графики y = f (x) и y =
g (x) пересекаются, оба графа имеют
точно такие же значения x и y. Итак, мы можем найти точку или точки
Итак, мы можем найти точку или точки
пересечения путем решения уравнения f (x)
= g (x). Решение этого уравнения даст нам значение (я) x
точка (и) пересечения. Затем мы можем найти значение y, поместив значение для
x, который мы нашли в одном из исходных уравнений.То есть путем расчета
либо f (x), либо g (x).
Пример 1
Рассчитать точку
пересечение двух прямых f (x) = 2x — 1 и g (x) = x + 1. Сначала
давайте посмотрим на график двух функций. Мы видим смысл
пересечение есть (2, 3).
Рассчитываем точку пересечения по
решение уравнения f (x) = g (x). То есть:
2х — 1 = х + 1
2х — х = 1 + 1
х = 2
Координата Y теперь может быть найдена
вычисление f (2):
f (2) = 2 × 2 — 1 =
3
Точка пересечения — (2,
3) .
Пример показывает, что мы можем найти точку
пересечения двумя способами.
Либо графически, нарисовав два графика в одной системе координат, либо
алгебраически, решив уравнение, такое как в приведенном выше примере.
Графическое решение уравнения легко с помощью
графический калькулятор или компьютерная программа, например Excel.
Некоторые уравнения нельзя решить алгебраически, но мы можем найти решения, которые
исправляем до любого количества значащих цифр, используя компьютеры и
калькуляторы.
Пример 2
Решите уравнение x 2 — 2x — 3 = 2x — 3 сначала графически, затем алгебраически.
Рисуем графики f (x) = x 2 —
2x — 3 и g (x) = 2x — 3 путем составления таблицы значений и построения графика
точки. Как из графика, так и из таблицы значений видно, что
графики пересекаются при x = 0 и x = 4 .
Решает алгебраически:
x 2 — 2x — 3 = 2x — 3
x 2 — 4x = 0
х (х — 4) = 0
Получение решений x = 0 и x = 4 .
Пример 3
Решите уравнение x 2 — 1 = 2x — 3
Сначала переместите все термины
перейдите к левой части уравнения и упростите.
Это дает x 2 — 2x + 2 = 0
Используем формулу корней квадратного уравнения с a = 1, b =
−2 и c = 2.
Число под знаком квадратного корня:
отрицательный, что означает, что это уравнение не имеет решения.
Чтобы понять, почему это так, мы рисуем графики в левой части оригинала.
уравнение
f (x) = x 2 — 1 и правая часть g (x) = 2x — 3.
Мы видим, что парабола
f (x) и прямая g (x) не пересекаются.Легко видеть, что мы
не может вычислить точку проникновения просто потому, что такой точки нет.
Пример 4
Решите уравнение x 3 — 3x + 2 = x 2 —
2x + 1
Как и в предыдущем примере, мы перемещаем все
слагаемые в левую часть уравнения.
x 3 — 3x + 2 = x 2 — 2x + 1
x 3 — x 2 — x + 1 = 0
(x 3 — x 2 ) — (x — 1) = 0
x 2 (x — 1) — (x — 1) = 0
(х — 1) (х 2 —
1) = 0
(х — 1) (х — 1) (х
+ 1) = 0
Расчеты показывают, что их всего два
решений, x = 1 и x = −1, но кубическое уравнение может иметь три
решения. График показывает нам, что происходит.
График показывает нам, что происходит.
Графики f (x) =
x 2 — 2x + 1 и g (x)
= x 3 — 3x + 2 пересекаются
только в двух местах, где x = −1 и x = 1, которые были решениями
уравнение.
Пример 5
Решите уравнение x 2 = x
Легко видеть, что x = 0 и x = 1 являются
решения уравнения, но есть ли еще решения? Это не очень
вероятно, но давайте посмотрим на графики.
Назовите левую часть f (x) = x 2 и правую часть g (x) = x.
Помните, что g (x) не может принимать отрицательные значения x, поэтому не может быть никаких
отрицательные точки пересечения.
На графике видно, что точек всего две
пересечения и, следовательно, только два решения уравнения. х = 0 и х =
1.
Вот как решить уравнение расчетом:
| x 2 = x х 4 = х х 4 — х = 0 x (x 3 — 1) = 0 | Квадрат обе стороны уравнения, чтобы избавиться от квадратного корня .  |
Это дает решение x = 0 и x = 1 .
Пример 6
Решите уравнение ln x = x 2 — 1
Это уравнение не так-то просто решить. Если мы
помните определение логарифма, мы видим, что x = 1 делает обе стороны
уравнение равно 0 и, следовательно, является одним решением уравнения. Мы рисуем
графики, чтобы увидеть, есть ли другие решения.
График показывает нам, что есть два
решения. Одно решение — ровно x
= 1, поскольку e 0 = 1.
Обратите внимание, что мы выбираем значения x так, чтобы значения y
становятся все ближе и ближе друг к другу в таблице значений. Таким образом мы
можем выбрать значение x, чтобы получить желаемую точность.
| Пример 7 | EXCEL |
Если мы воспользуемся графическим калькулятором, то сможем найти
решение уравнения ln x = x 2 — 1 намного проще. 2 − ln (B2)
2 − ln (B2)
Теперь выберите Инструменты
а затем «Поиск цели» в строке меню.В
на экране появляется следующее:
Пишем D2,
1 и B2 в промежутках, как показано. Мы просим Excel сделать значение ячейки D2 равным
к значению 1, изменив значение в B2.
Когда
нажимаем ОК, появляется следующая информация.
Это говорит нам о том, что
аппроксимация x ≈ 0,45, которую мы нашли графически в примере 6, довольно
хорошее решение x ≈ 0.4500289, найденный с помощью EXCEL, не намного лучше.
Попробуйте пройти тест 3 по уравнениям III.
Не забудьте использовать контрольный список для
следите за своей работой.
Тем по алгебре: Показатели
/ ru / algebra-themes / order-of-operations / content /
Что такое экспоненты?
Экспоненты — это числа, которые были умножены сами на себя. Например, 3 · 3 · 3 · 3 можно записать как показатель степени 3 4 : число 3 было умножено на само себя 4 раз.
Экспоненты полезны, потому что позволяют записывать длинные числа в сокращенной форме. Например, это число очень большое:
.
1 000 000 000 000 000 000
Но вы могли бы записать это как экспонента:
10 18
Он также работает с маленькими числами с большим количеством десятичных знаков. Например, это число очень маленькое, но состоит из множества цифр:
.00000000000000001
Его также можно было бы записать в виде экспоненты:
10 -17
Ученые часто используют экспоненты для обозначения очень больших и очень маленьких чисел.Вы также часто увидите их в задачах алгебры.
Показатели степени
Как вы видели на видео, экспоненты записываются так: 4 3 (вы бы прочитали это как 4 в 3-й степени ). Все показатели состоят из двух частей: основание , являющееся умножаемым числом; и степень , которая представляет собой количество раз, когда вы умножаете основание.
Поскольку наша база равна 4, а наша степень равна 3, нам нужно умножить 4 на само три раз.3. Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа используемого калькулятора — и особенно если вы используете калькулятор на своем телефоне или компьютере — вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его.
Показатели в 1-й и 0-й степени
Как бы вы упростили эти показатели?
7 1 7 0
Не расстраивайтесь, если вы запутались. Даже если вы чувствуете себя комфортно с другими показателями, непонятно, как их вычислять со степенями 1 и 0.К счастью, эти показатели следуют простым правилам:
- Показатели со степенью 1
Любая экспонента со степенью 1 равна основанию , поэтому 5 1 равно 5, 7 1 равно 7, а x 1 равно x .
- Показатели степени 0
Любой показатель степени со степенью 0 равен 1 , поэтому 5 0 равно 1, а также 7 0 , x 0 и любой другой показатель степени с мощностью 0 вы можете думать.
Операции с показателями
Как бы вы решили эту проблему?
2 2 ⋅ 2 3
Если вы думаете, что вам нужно сначала решить экспоненты, а затем перемножить полученные числа, вы правы. (Если вы не уверены, ознакомьтесь с нашим уроком о порядке действий).
Как насчет этого?
x 3 / x 2
Или этот?
2x 2 + 2x 2
Хотя вы не можете точно решить эти проблемы без дополнительной информации, вы можете упростить , их.В алгебре вас часто просят выполнить вычисления показателей степени с переменными в качестве основы. К счастью, эти показатели легко складывать, вычитать, умножать и делить.
Сложение показателей
Когда вы добавляете два показателя степени, вы не добавляете действительные силы — вы добавляете основания. Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x 2 + x 2 будет 2x 2 .
x 2 + x 2 = 2x 2
Как насчет этого выражения?
3 года 4 + 2 года 4
Вы добавляете 3y к 2y. Поскольку 3 + 2 равно 5, это означает, что 3y 4 + 2y 4 = 5y 4 .
3 года 4 + 2 года 4 = 5 лет 4
Вы могли заметить, что мы рассматривали только те задачи, в которых добавляемые показатели имели одинаковую переменную и мощность.Это потому, что вы можете добавлять экспоненты, только если их основания и экспоненты точно такие же, как . Таким образом, вы можете добавить их ниже, потому что оба члена имеют одинаковую переменную ( r ) и одинаковую мощность (7):
Таким образом, вы можете добавить их ниже, потому что оба члена имеют одинаковую переменную ( r ) и одинаковую мощность (7):
4к 7 + 9к 7
Вы не можете никогда, добавлять что-либо из них в том виде, в каком они написаны. В этом выражении есть переменные с двумя разными степенями:
4к 3 + 9 8
У этого есть те же возможности, но разные переменные, поэтому вы также не можете добавить его:
4к 2 + 9с 2
Вычитание показателей
Вычитание экспонент работает так же, как их сложение.Например, вы можете придумать, как упростить это выражение?
5x 2 — 4x 2
5-4 равно 1, поэтому, если вы сказали 1 x 2 или просто x 2 , вы правы. Помните, что, как и при сложении показателей, вы можете вычитать только показатели с такой же степенью и основанием .
5x 2 — 4x 2 = x 2
Показатели умножения
Умножить экспоненты просто, но способ, которым вы это делаете, может вас удивить.Чтобы умножить степень, сложите степени . Например, возьмите это выражение:
x 3 ⋅ x 4
Степени: 3 и 4 . Поскольку 3 + 4 равно 7, мы можем упростить это выражение до x 7 .
x 3 ⋅ x 4 = x 7
А как насчет этого выражения?
3x 2 ⋅ 2x 6
Степени равны 2 и 6 , поэтому наша упрощенная экспонента будет иметь степень 8.В этом случае нам также потребуется умножить коэффициенты. Коэффициенты равны 3 и 2. Нам нужно умножить их, как и любые другие числа. 3⋅2 равно 6 , поэтому наш упрощенный ответ: 6x 8 .
3x 2 ⋅ 2x 6 = 6x 8
Вы можете упростить умножение экспоненты только с той же переменной. Например, выражение 3x 2 ⋅2x 3 ⋅4y 2 будет упрощено до 24x 5 ⋅y 2 .Для получения дополнительной информации перейдите к нашему уроку «Упрощение выражений».
Показатели деления
Деление показателей аналогично их умножению. Вместо того, чтобы складывать степени, вы из вычитаете их . Возьмите это выражение:
х 8 / х 2
Поскольку 8-2 равно 6, мы знаем, что x 8 / x 2 равно x 6 .
x 8 / x 2 = x 6
Что насчет этого?
10x 4 / 2x 2
Если вы думаете, что ответ — 5x 2 , вы правы! 10/2 дает нам коэффициент 5, а вычитание степеней ( 4 — 2 ) означает, что степень равна 2.
Возведение власти в степень
Иногда можно увидеть такое уравнение:
(х 5 ) 3
Показатель степени на другой экспоненте может сначала показаться запутанным, но у вас уже есть все навыки, необходимые для упрощения этого выражения. Помните, что показатель степени означает, что вы умножаете основание на само на себя столько раз. Например, 2 3 это 2⋅2⋅2. Это означает, что мы можем переписать (x 5 ) 3 как:
x 5 x 5 ⋅x 5
Чтобы умножить экспоненты с одинаковым основанием, просто сложите показателей.Следовательно, x 5 ⋅x 5 ⋅x 5 = x 5 + 5 + 5 = x 15 .
На самом деле есть еще более короткий способ упростить подобные выражения. Взгляните еще раз на это уравнение:
(x 5 ) 3 = x 15
Вы обратили внимание, что 5⋅3 тоже равно 15? Помните, умножение — это то же самое, что и более одного сложения чего-либо. Это означает, что мы можем представить 5 + 5 + 5, как мы делали раньше, как 5 умножить на 3.Следовательно, когда вы возводите степень в степень , вы можете на умножить степень .
Это означает, что мы можем представить 5 + 5 + 5, как мы делали раньше, как 5 умножить на 3.Следовательно, когда вы возводите степень в степень , вы можете на умножить степень .
Рассмотрим еще один пример:
(х 6 ) 4
Так как 6⋅4 = 24, (x 6 ) 4 = x 24
х 24
Рассмотрим еще один пример:
(3x 8 ) 4
Во-первых, мы можем переписать это как:
3x 8 ⋅3x 8 ⋅3x 8 ⋅3x 8
Помните, что при умножении порядок не имеет значения.Поэтому мы можем переписать это снова как:
3⋅3⋅3⋅3⋅x 8 ⋅x 8 ⋅x 8 ⋅x 8
Поскольку 3⋅3⋅3⋅3 = 81 и x 8 ⋅x 8 ⋅x 8 ⋅x 8 = x 32 , наш ответ:
81x 32
Обратите внимание, это также было бы то же самое, что и 3 4 ⋅x 32 .

 При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;